Ghép cặp, Bình quân Gia quyền hay Hồi quy
Nguồn: Biên tâp lại từ Matteo Courthoud theo Towardsdatascience
! pip install causalml
import numpy as np
import pandas as pd
import statsmodels.formula.api as smf
import seaborn as sns
Hiểu và so sánh các phương pháp suy luận nhân quả có điều kiện.
Phép thử A/B hoặc thử nghiệm kiểm soát ngẫu nhiên là tiêu chuẩn vàng trong suy luận nhân quả. Bằng cách phân ngẫu nhiên các cá nhân vào nhóm (nhận) can thiệp hoặc đối chứng, ta có thể an tâm rằng cá nhân bình quân trong hai nhóm này tương tự nhau và mọi khác biệt ta quan sát được có thể quy hoàn toàn cho tác động của can thiệp.
Tuy nhiên nhóm can thiệp và đối chứng nhiều khi không hoàn toàn tương đồng. Lý do có thể vì quá trình phân bổ ngẫu nhiên không hoàn hảo hoặc không thể tiến hành. Vì các lý do đạo đức hoặc các lý do thực tiễn khác, không phải lúc nào ta cũng có thể phân bổ can thiệp một cách ngẫu nhiên. Ngay cả khi có thể, đôi khi ta không có mẫu quan sát đủ lớn để có thể nhận ra sự khác biệt giữa hai nhóm. Ví dụ điều này thường xảy ra khi quá trình ngẫu nhiên hóa không được thực hiện ở cấp độ cá nhân mà ở cấp độ nhóm gộp, ví dụ mã địa chỉ, quận/huyện hoặc tỉnh thành phố.
Trong các hoàn cảnh này, ta vẫn có thể khôi phục ước lượng nhân quả của tác động can thiệp sau khi can thiệp đã diễn ra nếu ta có đủ thông tin về các cá nhân bằng cách làm cho nhóm can thiệp và đối chứng trở nên tương tự nhau. Trong bài viết này, chúng ta sẽ cùng tìm hiểu và so sánh các quy trình ước lượng tác động nhân quả khi có sự mất cân xứng giữa nhóm can thiệp và đối chứng mà ta quan sát được toàn bộ. Cụ thể, chúng ta sẽ phân tích dữ liệu sử dụng ba phương pháp: ghép cặp, bình quân gia quyền và hồi quy.
Ví dụ
Giả sử ta có một trang blog về thống kê và suy luận nhân quả 😇. Để nâng cao trải nhiệm người dùng, ta cân nhắc việc sử dụng chế độ nền tối và muốn tìm hiểu liệu tính năng này có làm tăng thời gian người dùng dành cho trang blog hay không.

Chúng ta không phải một công ty lớn, vì thế chúng ta không chạy phép thử A/B mà chỉ đơn giản tung ra phiên bản nền tối và quan sát người dùng chọn nó hay không và thời gian họ dành cho trang blog. Chúng ta biết rằng có sự [tự] chọn lựa ở đây: những người dùng thích chế độ nền tối có thể cũng đồng thời có các sở thích đọc khác và điều này có thể cản trở phân tích nhân quả.
Chúng ta có thể biểu diễn mô hình tạo lập dữ liệu bằng Biểu đồ Chỉ hướng Không Tuần Hoàn (Directed Acyclic Graph (DAG)).
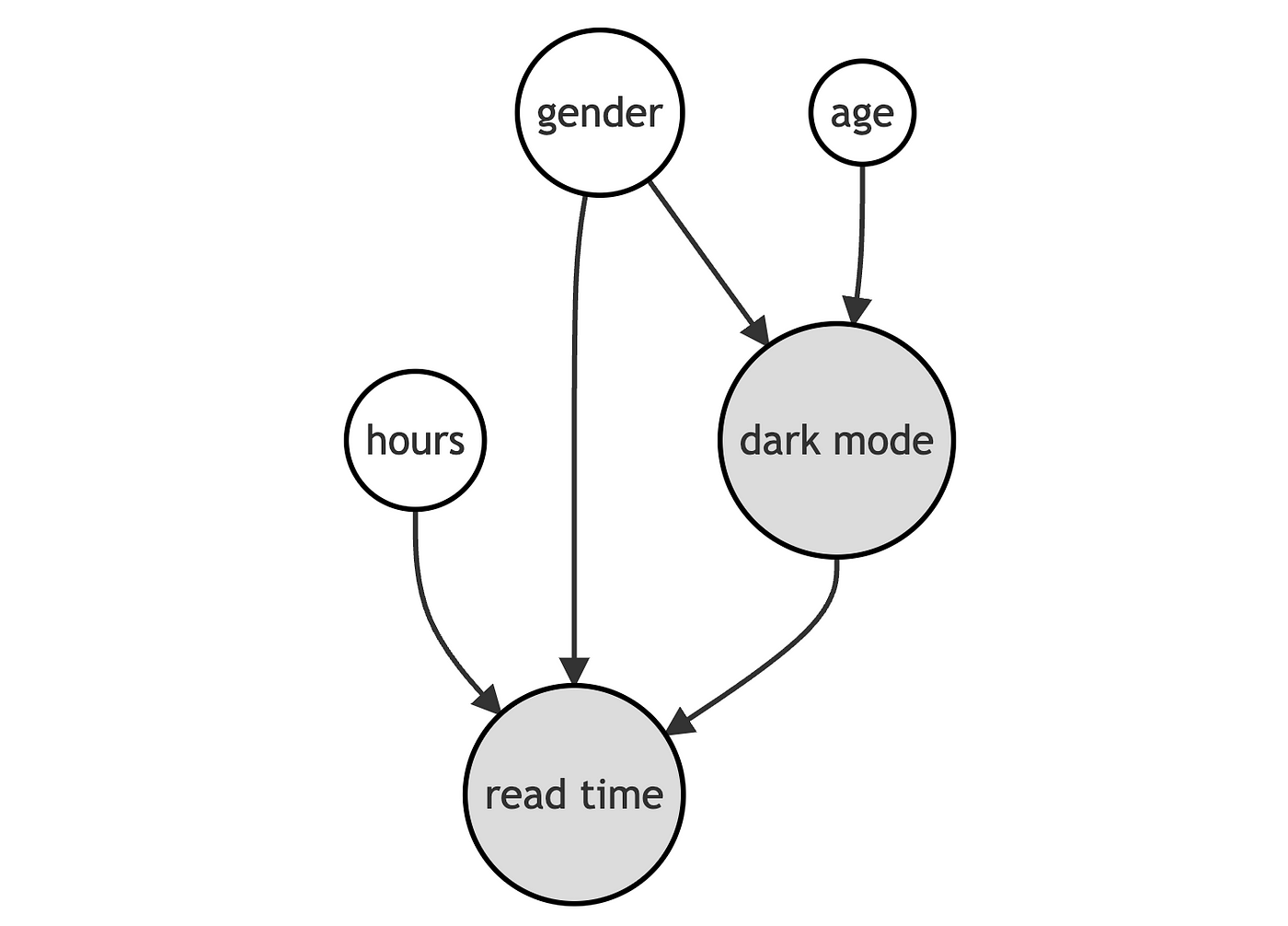
Chúng ta tạo lập dữ liệu mô phỏng sử dụng mô hình tạo lập dữ liệu như sau:
class dgp_darkmode():
"""
Data Generating Process: blog dark mode and time spend reading
"""
def generate_data(self, N=300, seed=1):
np.random.seed(seed)
# Control variables
nam_giới = np.random.binomial(1, 0.45, N)
tuổi = np.rint(18 + np.random.beta(2, 2, N)*50)
tổng_giờ_đọc = np.minimum(np.round(np.random.lognormal(5, 1.3, N), 1), 2000)
# Treatment
pr = np.maximum(0, np.minimum(1, 0.8 + 0.3*nam_giới - np.sqrt(tuổi-18)/10))
nền_tối = np.random.binomial(1, pr, N)==1
# Outcome
số_giờ_đọc = np.round(np.random.normal(10 - 4*nam_giới + 2*np.log(tổng_giờ_đọc) + 2*nền_tối, 4, N), 1)
# Generate the dataframe
df = pd.DataFrame({'số_giờ_đọc': số_giờ_đọc, 'nền_tối': nền_tối, 'nam_giới': nam_giới, 'tuổi': tuổi, 'tổng_giờ_đọc': tổng_giờ_đọc})
return df
df = dgp_darkmode().generate_data()
df.head()
| số_giờ_đọc | nền_tối | nam_giới | tuổi | tổng_giờ_đọc | |
|---|---|---|---|---|---|
| 0 | 14.4 | False | 0 | 43.0 | 65.6 |
| 1 | 15.4 | False | 1 | 55.0 | 125.4 |
| 2 | 20.9 | True | 0 | 23.0 | 642.6 |
| 3 | 20.0 | False | 0 | 41.0 | 129.1 |
| 4 | 21.5 | True | 0 | 29.0 | 190.2 |
Ta có thông tin về 300 người dùng. Ta có thể quan sát họ chọn chế độ nền_tối (can thiệp) hay không, thời gian đọc hàng tuần số_giờ_đọc (biến kết quả) và các đặc điểm như giới tính, tuổi và tổng thời gian đã dành cho blog.
Ta muốn ước lược tác động của nền_tối lên số_giờ_đọc của người dùng. Nếu ta có thể chạy phép thử A/B hoặc thử nghiệm ngẫu nhiên , ta chỉ việc so sánh người đọc sử dụng và không sử dụng chế độ nền tối và quy khác biệt về số giờ đọc bình quân cho nền_tối. Hãy cùng kiểm tra con số mà ta có:
df.query('nền_tối==True').số_giờ_đọc.mean()-df.query('nền_tối==False').số_giờ_đọc.mean()
-0.4446330948042103
Người dùng chọn nền_tối trung bình đọc blog ít hơn 0.44 giờ mỗi tuần. Liệu ta có thể kết luận nền_tối là một ý tưởng tồi? Đây có phải tác động nhân quả hay không?
Ta không phân ngẫu nhiên nền_tối vì thế người dùng chọn lựa nó không hoàn toàn giống người dùng không chọn. Liệu ta có thể kiểm chứng lo ngại này? Một phần nào đó. Ta chỉ có thể kiểm tra các thuộc tính có thể quan sát như giới tính, tuổi tác và tổng số giờ trong thiết lập của mình. Ta không thể kiểm tra liệu người đọc có khác biệt dựa trên các thuộc tính không quan sát được.
Hãy dùng hàm create_table_one từ thư viện causalml của Uber để lập bảng so sánh thuộc tính, bao gồm giá trị trung bình các đặc điểm của người dùng giữa hai nhóm kiểm soát và can thiệp. Như tên của nó gợi mở, chúng ta nên trình bảy bảng này ngay khi bắt đầu phân tích suy luận nhân quả.
from causalml.match import create_table_one
X = ['nam_giới', 'tuổi', 'tổng_giờ_đọc']
table1 = create_table_one(df, 'nền_tối', X)
table1
| Control | Treatment | SMD | |
|---|---|---|---|
| Variable | |||
| n | 151 | 149 | |
| nam_giới | 0.34 (0.47) | 0.66 (0.48) | 0.6732 |
| tuổi | 46.01 (9.79) | 39.09 (11.53) | -0.6469 |
| tổng_giờ_đọc | 337.78 (464.00) | 328.57 (442.12) | -0.0203 |
Có nhiều khác biệt giữa nhóm can thiệp và đối chứng. Cụ thể người dùng lựa chọn nền_tối trẻ hơn, dành ít thời gian đọc blog hơn và nhiều khả năng là nam.
Một cách khác để biểu diễn tất cả khác biệt cùng một lúc là sử dùng biểu đồ violin theo cặp. Ưu điểm của biểu đồ này là cho phép ta quan sát toàn bộ phân phối xác suất của biến (xấp xỉ thông qua ước lượng mật độ kernel)
def plot_distributions(df, X, d):
import seaborn as sns
df_long = df.copy()[X + [d]]
df_long[X] =(df_long[X] - df_long[X].mean()) / df_long[X].std()
df_long = pd.melt(df_long, id_vars=d, value_name='value')
sns.violinplot(y="variable", x="value", hue=d, data=df_long, split=True).\
set(xlabel="", ylabel="", title="Normalized Variable Distribution");
plot_distributions(df, X, "nền_tối")
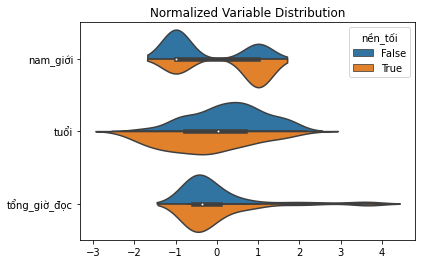
Kết luận đưa ra từ biểu đồ violin khá tương đồng: người dùng lựa chọn nền_tối dường như rất khác các người dùng khác.
Tại sao phải để tâm?
Nếu ta không kiểm soát các thuộc tính quan sát được, ta không thể ước lượng tác động can thiệp thực. Nói ngắn gọn, ta không thể chắc rằng, khác biệt trong kết quả, số_giờ_đọc, có thể quy cho tác động, nền_tối, thay vì các thuộc tính khác. Ví dụ, có khả năng nam giới đọc ít hơn và đồng thời thích nền_tối hơn, vì thế ta quan sát thấy tương quan ngược chiều ngay cả khi nền_tối không có tác động đối với số_giờ_đọc (hoặc thậm chí mối quan hệ thực có thể là cùng chiều).
Nói theo ngôn ngữ Biểu đồ Chỉ hướng Không Tuần Hoàn (DAG), điều này có nghĩa là ta có một lối đi cửa sau cần được đóng lại để có thể phân tích nhân quả.
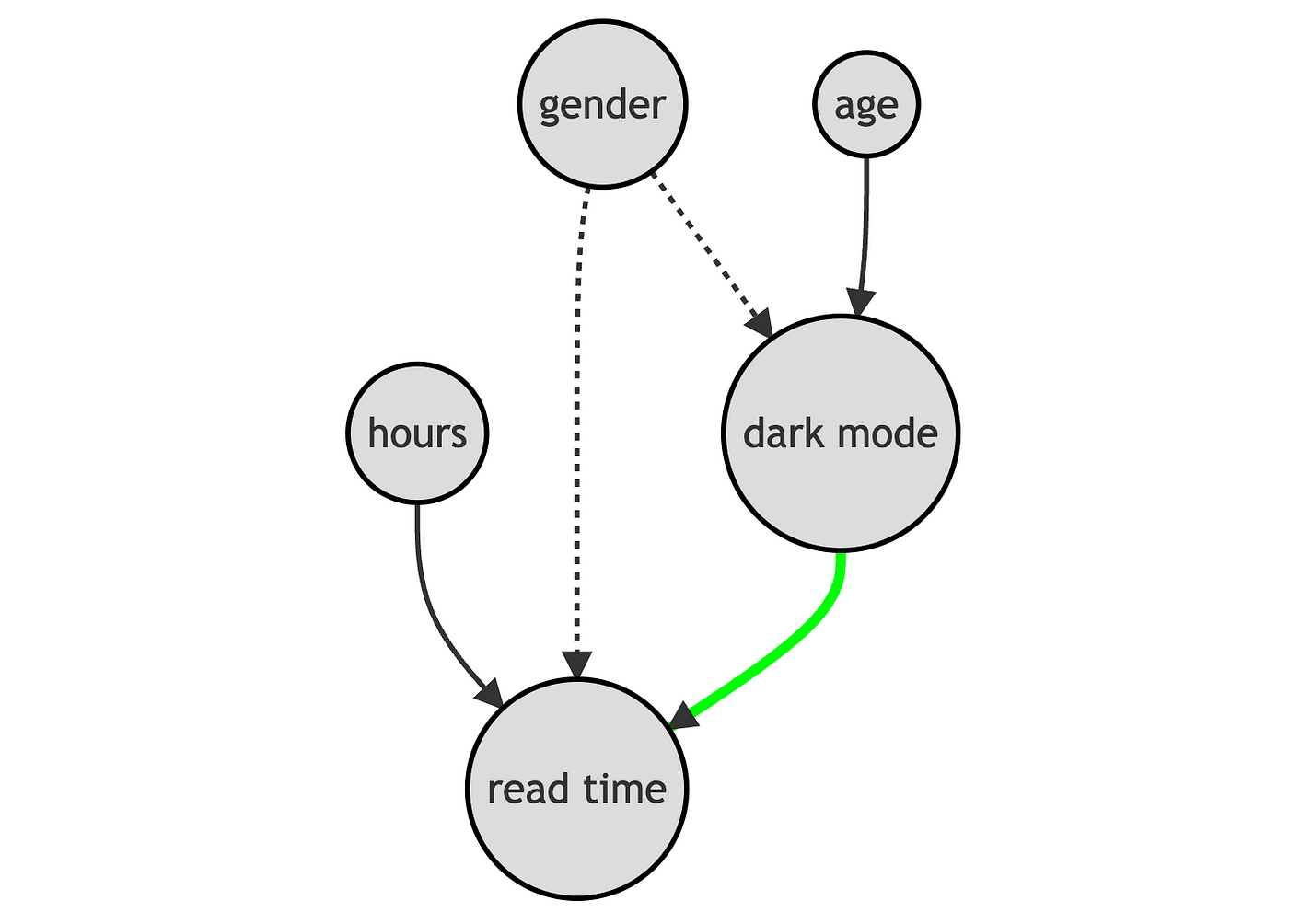
Làm thế nào để ta phân tích điều kiện với các biến giới tính, tuổi tác và số giờ đọc? Ta có một vài lựa chọn như sau:
- Ghép cặp
- Bình quân gia quyền theo điểm xu hướng
- Hồi quy với biến kiểm soát
Hãy cùng khám phá và so sánh chúng!
Phân tích điều kiện
Giả sử với một tập hợp các đối tượng i = 1, …, n, ta quan sát được bộ số (Dᵢ, Yᵢ, Xᵢ) bao gồm:
- Biến phân bổ can thiệp $D_i ∈ {0,1}$ (nền_tối)
- Biến kết quả $Y_i ∈ ℝ$ (số_giờ_đọc)
- Vector các biến thuộc tính $X_i ∈ ℝ^n$ (gender, tuổi and tổng_giờ_đọc)
Giả thiết 1: Không có nhiễu (hoặc có thể bỏ qua [các biến không quan sát được], hoặc lựa chọn theo các biến quan sát được)

nghĩa là khi cố định các thuộc tính quan sát được X, việc phân bổ can thiệp D gần như ngẫu nhiên. Về bản chất, ta giả thiết rằng không có thuộc tính không quan sát được nào ảnh hưởng đồng thời đến việc người dùng chọn nền_tối và số_giờ_đọc của họ. Đây là một giả thiết khá mạnh và nhiều khả năng hợp lý khi ta quan sát được nhiều thuộc tính của các đối tượng.
Giả thiết 2: Trùng lặp (hoặc [có] vùng hỗ trợ chung)

nghĩa là không đối tượng nào được chắc chắn phân vào nhóm can thiệp hoặc đối chứng. Đây là một giả thiết mang tính kĩ thuật, hàm ý, tại mọi giá trị của giới tính, tuổi tác và số giờ, luôn tồn tại cả người đọc lựa chọn nền_tối và người đọc không chọn chế độ này. Khác với giả thiết không có nhiễu, giả thiết trùng lặp có thể được kiểm chứng.
Ghép cặp
Phương pháp đầu tiên và có lẽ trực quan nhất là tiến hành phân tích điều kiện bằng ghép cặp.
Ý tưởng ghép cặp rất đơn giản. Ví dụ, ta không chắc chắn, ví dụ người dùng giới tính nam và nữ có tương đồng, ta phân tích theo từng giới. Thay vì so sánh số_giờ_đọc theo giá trị biến nền_tối cho toàn bộ mẫu dữ liệu, ta chia nhỏ chúng theo người dùng nam và nữ.
df_gender = pd.pivot_table(df, values='số_giờ_đọc', index='nam_giới', columns='nền_tối', aggfunc=np.mean)
df_gender['diff'] = df_gender[1] - df_gender[0]
df_gender
| nền_tối | False | True | diff |
|---|---|---|---|
| nam_giới | |||
| 0 | 20.318000 | 22.24902 | 1.931020 |
| 1 | 16.933333 | 16.89898 | -0.034354 |
Bây giờ tác động của nền_tối có vẻ đổi chiều: âm cho người dùng nam (-0.03) nhưng dương với trị số lớn cho người dùng nữ (+1.93). Tác động cộng gộp dương, 1.93-0.03=1.90 (giả sử tỉ lệ giới tính cân bằng)! Hiện tượng đổi dấu là một ví dụ cổ điển của Nghịch lý Simpson’s.
Phép so sánh này có thể thực hiện dễ dàng cho giới tính vì nó là biến nhị phân. Với nhiều biến, đôi khi bao gồm cả biến liên tục, ghép cặp trở nên khó khăn hơn. Một chiến lược phổ biến là ghép cặp người dùng trong nhóm can thiệp với người dùng gần giống nhất trong nhóm kiểm soát, sử dụng một thuật toán láng giềng gần nhất nào đó. Chúng ta sẽ không đi sâu diễn giải thuật toán ở đây nhưng ta có thể thực hiện ghép cặp với hàm NearestNeighborMatch từ gói causalml.
Hàm NearestNeighborMatch tạo ra một bộ dữ liệu nơi người dùng trong nhóm can thiệp được ghép 1:1 (tham số ratio=1) với các người dùng trong nhóm đối chứng.
from causalml.match import NearestNeighborMatch
psm = NearestNeighborMatch(replace=True, ratio=1, random_state=1)
df_matched = psm.match(data=df, treatment_col="nền_tối", score_cols=X)
Liệu hai nhóm có thực sự trở ên tương xứng? Ta có thể tạo một phiên bản mới của bảng cân đối
table1_matched = create_table_one(df_matched, "nền_tối", X)
table1_matched
| Control | Treatment | SMD | |
|---|---|---|---|
| Variable | |||
| n | 104 | 104 | |
| nam_giới | 0.62 (0.49) | 0.62 (0.49) | 0.0 |
| tuổi | 41.93 (10.05) | 41.85 (10.02) | -0.0086 |
| tổng_giờ_đọc | 206.92 (309.62) | 209.48 (321.79) | 0.0081 |
Bây giờ khác biệt bình quân giữa hai nhóm giảm nhiều lần. Tuy nhiên lưu ý cỡ mẫu giảm nhẹ (300-208) vì (1) ta chỉ ghép cặp cho các người dùng chịu tác động bởi can thiệp và (2) ta không thể tìm được phương án ghép tốt cho toàn bộ người dùng này.
Ta có thể biểu diễn khác biệt về phân phối xác suất với biểu đồ violin theo cặp.
plot_distributions(df_matched, X, "nền_tối")
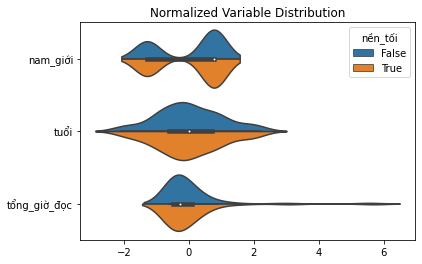
Một cách phổ biến để biểu diễn tính cân bằng của các biến giải thích trước và sau ghép cặp là sử dụng biểu đồ cân bằng. Biểu đồ này trình bày hiệu kì vọng chuẩn hóa trước và sau ghép cặp cho mỗi biến kiểm soát.
def plot_balance(t1, t2, X):
import seaborn as sns
import matplotlib.pyplot as plt
df_smd = pd.DataFrame({"Variable": X + X,
"Sample": ["Unadjusted" for _ in range(len(X))] + ["Adjusted" for _ in range(len(X))],
"Standardized Mean Difference": t1["SMD"][1:].to_list() +
t2["SMD"][1:].to_list()})
sns.scatterplot(x="Standardized Mean Difference", y="Variable", hue="Sample", data=df_smd).\
set(title="Balance Plot")
plt.axvline(x=0, color='k', ls='--', zorder=-1, alpha=0.3);
plot_balance(table1, table1_matched, X)
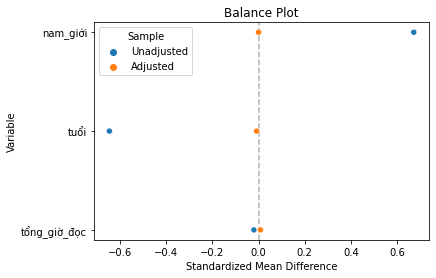
Ta có thể thấy, tất cả khác biệt về thuộc tính quan sát được giữa hai nhóm gần như bằng không. Ta cũng có thể sso sánh các phân phối xác suất sử dụng các thang đo và kiểm định thống kế, ví dụ kiểm định thống kê Kolmogorov-Smirnov.
Làm thế nào để ước lượng tác động can thiệp? Ta chỉ việc đơn giản tính hiệu của kì vọng. Một cách tương đương đồng thời cung cấp sai số chuẩn là chạy hồi quy tuyến tính biến kết quả số_giờ_đọc, theo can thiệp, nền_tối.
Lưu ý vì chúng ta đã ghép cặp cho từng người dùng nhận can thiệp, tác động can thiệp mà ta ước lượng là tác động can thiệp bình quân đối với nhóm can thiệp. Đại lượng này có thể khác tác động can thiệp bình qân nếu nhóm can thiệp khác với quần thể chung (điều này nhiều khả năng xảy ra nếu không chúng ta đã không cần ghép gặp).
smf.ols("số_giờ_đọc ~ nền_tối", data=df_matched).fit().summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 17.0365 | 0.469 | 36.363 | 0.000 | 16.113 | 17.960 |
| nền_tối[T.True] | 1.4490 | 0.663 | 2.187 | 0.030 | 0.143 | 2.755 |
Tác động trở nên dương và có ý nghĩa thống kê ở mức 5%.
Lưu ý là ta có thể ghép nhiều người dùng chịu ảnh hưởng với các người dùng tương tự không chịu ảnh hưởng của can thiệp. Điều này vi phạm giả thiết độc lập giữa các quan sát và làm sai lệch phân tích. Ta có 2 giải pháp:
- Nhóm cụm sai số chuẩn theo cá nhân trước khi ghép cặp.
- Tính sai số chuẩn bằng bootstrap (phù hợp hơn).
Dưới đây ta thực hiện giải pháp thứ nhất và nhóm cụm sai số chuẩn theo mã số cá nhân ban đầu (chỉ số khung dữ liệu).
smf.ols("số_giờ_đọc ~ nền_tối", data=df_matched)\
.fit(cov_type='cluster', cov_kwds={'groups': df_matched.index})\
.summary().tables[1]
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 17.0365 | 0.650 | 26.217 | 0.000 | 15.763 | 18.310 |
| nền_tối[T.True] | 1.4490 | 0.821 | 1.765 | 0.078 | -0.160 | 3.058 |
Tác động trở lên ít có ý nghĩa thống kê hơn.
Điểm xu hướng
Rosenbaum and Rubin (1983) chứng minh một kết quả rất mạnh: với giả thiết có thể bỏ qua (dạng mạnh), việc phân tích điều kiện theo xác suất nhận can thiệp (điểm xu hướng) đủ để đảm bảo tính độc lập có điều kiện.

Trong đó e(Xᵢ) là xác suất nhận can thiệp của cá nhân i khi cố định các thuộc tính quan sát được Xᵢ.

Lưu ý trong phép thử A/B, điểm xu hướng là giống nhau cho các cá nhân.
Kết quả của Rosenbaum and Rubin (1983) rất mạnh và hữu ích vì điểm xu hướng là biến một chiều, trong khi biến kểm soát X có thể là dữ liệu nhiều chiều.
Với giả định không có nhiễu giới thiệu ở trên, ta có thể viết lại tác động can thiệp bình quân như sau:
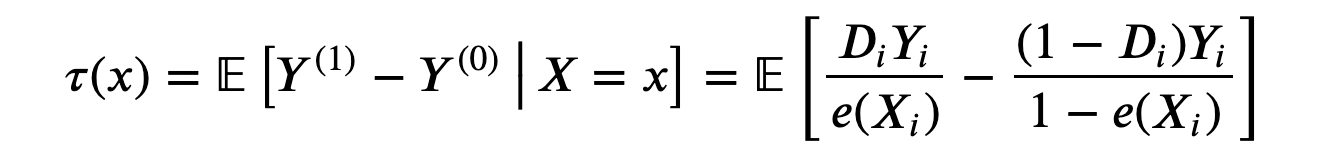
Lưu ý là công thức tác động can thiệp bình quân này không phụ thuộc vào các kết quả tiềm năng Yᵢ⁽¹⁾ and Yᵢ⁽⁰⁾, mà chỉ phụ thuộc vào kết quả quan sát Yᵢ.
Công thức tác động can thiệp bình quân này hàm ý rằng ước lượng Bình quân Gia quyền theo nghịch đảo của điểm xu hướng (Inverse Propensity Weighted - IPW) là ước lượng không chệch của tác động can thiệp bình quân τ.
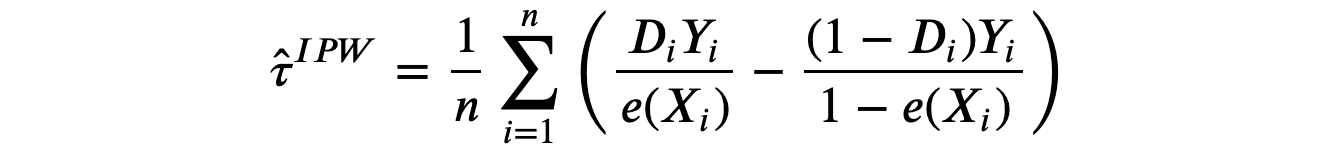
Ước lượng này không khả thi vì ta không quan sát được điểm xu hướng e(Xᵢ). Tuy nhiên, ta có thể ước lượng chúng. Trên thực tế Imbens, Hirano, Ridder (2003) chỉ ra rằng bạn nên sử dụng giá trị ước lượng của điểm xu hướng ngay cả khi bạn biết giá trị thật của chúng (ví dụ nếu bạn biết quy trình lấy mẫu). Ý tưởng là, nếu ước lượng của điểm xu hướng khác giá trị thực của chúng, điều này mang thêm thông tin cho quá trình ước lượng.
Có nhiều cách để ước lượng xác suất, và cách đơn giản và phổ biến nhất là sử dụng hồi quy logistic.
from sklearn.linear_model import LogisticRegressionCV
df["pscore"] = LogisticRegressionCV().fit(y=df["nền_tối"], X=df[X]).predict_proba(df[X])[:,1]
Bất cứ khi nào xây dựng mô hình dự đoán, ta nên xây dựng mô hình dựa trên mẫu dữ liệu khác với dữ liệu dùng để suy luận. Nguyên tắc này thường được gọi là đánh giá chéo hoặc ước lượng chéo. Một trong những quy trình đánh giá chéo tốt nhất (nhưng tính toán nhiều) là ước lượng chéo bỏ một quan sát (leave-one-out LOO): khi dự đoán giá trị của quan sát i, ta sử dụng toàn bộ dữ liệu ngoại trừ i. Ta thực hiện quy trình ước lượng chéo LOO sử dụng các hàm cross_val_predict và LeaveOneOut của thư viện Sklearn.
from sklearn.model_selection import cross_val_predict, LeaveOneOut
df['pscore'] = cross_val_predict(estimator=LogisticRegressionCV(),
X=df[X],
y=df["nền_tối"],
cv=LeaveOneOut(),
method='predict_proba',
n_jobs=-1)[:,1]
Một phép thử quan trọng sau khi ước lượng điểm xu hướng là vẽ đồ thị so sánh nhóm can thiệp và đối chứng. Trước hết, ta có thể quan sát xem hai nhóm có cân bằng hay không dựa vào việc quan sát hai phân phối xác suất có tương tự hay không. Hơn nữa, ta có thể kiểm tra giả thiết trùng lặp có thỏa đáng hay không. Trường hợp lý tưởng là hai phân phối xác suất cùng phủ khoảng giá trị.
sns.histplot(data=df, x='pscore', hue='nền_tối', bins=30, stat='density', common_norm=False).\
set(ylabel="", title="Distribution of Propensity Scores");
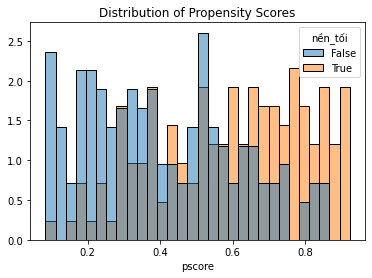
Như dự kiến, phân phối xác suất điểm xu hướng giữa nhóm can thiệp và kiểm soát rất khác nhau, hàm ý hai nhóm không tương đồng. Tuy nhiên hai phân phối xác suất cùng phủ một khoảng giá trị tương tự, hàm ý giả thiết trùng lặp được tuân thủ.
Làm thế nào để ước lượng tác động can thiệp bình quân?
Sau khi tính điểm xu hướng, ta chỉ việc gán quyền số cho các quan sát bằng điểm xu hướng của chúng. Chúng ta có thể tính hiệu của bình quân gia quyền của số_giờ_đọc hoặc chạy một phương trình hồi quy gia quyền của số_giờ_đọc theo nền_tối sử dụng hàm wls (bình phương tối thiểu gia quyền)
w = 1 / (df["pscore"] * df["nền_tối"] + (1-df["pscore"]) * (1-df["nền_tối"]))
smf.wls("số_giờ_đọc ~ nền_tối", weights=w, data=df).fit().summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 18.5755 | 0.412 | 45.131 | 0.000 | 17.766 | 19.386 |
| nền_tối[T.True] | 1.1242 | 0.582 | 1.930 | 0.054 | -0.022 | 2.270 |
The effect of nền_tối is now positive and almost statistically significant, at the 5% level.
Note that the wls function automatically normalizes weights so that they sum to 1, which greatly improves the stability of the estimator. In fact, the unnormalized IPW estimator can be very unstable when the propensity scores approach zero or one.
Tác động của nền_tối trở nên dương và gần có ý nghĩa thống kê ở mức 5%.
Lưu ý hàm wls tự động chuẩn hóa các quyền số sao cho tổng của chúng bằng 1. Điều này giúp làm tăng tính vững của ước lượng. Trên thực tế, ước lượng IPW không chuẩn hóa có thể trở nên rất không vững khi điểm xu hướng tiến tới 1 hoặc 0.
Hồi quy với Biến Kiểm soát
Phương pháp cuối cùng mà ta xem xét hôm nay là hồi quy tuyến tính với biến kiểm soát. Ước lượng này rất dễ tiến hành vì ta chỉ việc đưa cá đặc điểm của người dùng - giới tính, tuổi và giờ vào phương trình hồi quy số_giờ_đọc theo nền_tối.
smf.ols("số_giờ_đọc ~ nền_tối + nam_giới + tuổi + tổng_giờ_đọc", data=df).fit().summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 16.8591 | 1.082 | 15.577 | 0.000 | 14.729 | 18.989 |
| nền_tối[T.True] | 1.3858 | 0.524 | 2.646 | 0.009 | 0.355 | 2.417 |
| nam_giới | -4.4855 | 0.499 | -8.990 | 0.000 | -5.468 | -3.504 |
| tuổi | 0.0513 | 0.022 | 2.311 | 0.022 | 0.008 | 0.095 |
| tổng_giờ_đọc | 0.0043 | 0.001 | 8.427 | 0.000 | 0.003 | 0.005 |
Tác động can thiệp bình quân lại mang dấu dương và có ý nghĩa thống kê ở mức 1%!
So sánh
Các phương pháp khác nhau ở trên có quan hệ như thế nào?
IPW và Hồi quy
Có một mối quan hệ chặt chẽ giữa ước ượng IPW và hồi quy tuyến tính với biến kiểm soát. Điều này càng rõ ràng khi ta có một biến rời rạc X.
Trong trường hợp này, giá trị ước lượng IPW được tính theo công thức:

Giá trị ước lượng IPW là bình quân gia quyền của tác động can thiệp τₓ, với quyền số là xác suất nhận can thiệp.
Giá trị ước lượng của hồi quy tuyến tính với biến kiểm soát là:
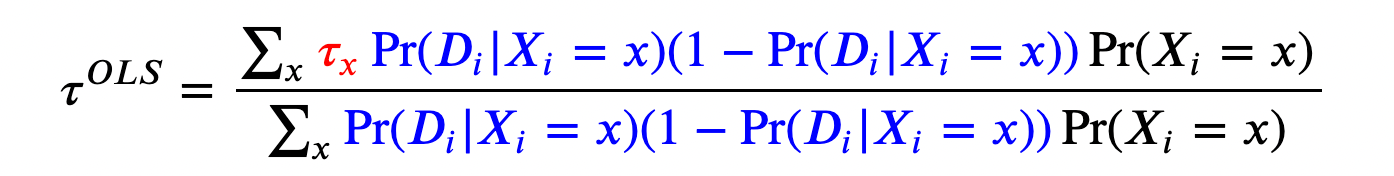
Giá trị ước lượng OLS là bình quân gia quyền của tác động can thiệp τₓ, với trọng số là phương sai của xác suất can thiệp. Điều này có nghĩa là hồi quy tuyến tính cũng là một ược lượng theo trọng số, với trọng số cao cho các thuộc tính mà ta quan sát được độ phân tán cao trong việc nhận tác động. Vì một biến ngẫu nhiên nhị phân có phương sai cao nhất tại giá trị kì vọng 0.5, OLS đặt trọng số cao cho các quan sát có đặc điểm quan sát được chia đều 50/50 giữa nhóm can thiệp và đối chứng. Mặt khác, nếu một số đặc điểm nào đó mà ta chỉ quan sát được ở nhóm can thiệp hoặc đối chứng, chúng sẽ nhận giá trị trọng số bằng 0. Tôi để cử chương 3 của cuốn sách Angrist and Pischke (2009) có thể cung cấp thêm chi tiết.
IPW và ghép cặp
Như ta thấy ở phần IPW, kết quả của Rosenbaum and Rubin (1983) cho thấy ta không nên tiến hành phân tích điều kiện với toàn bộ thuộc tính quan sát X, mà chỉ cần cố định điểm xu hướng e(X).
Ta đã thấy kết quả này không chỉ hàm ý ước lượng bình quân gia quyền mà còn mở rộng cho ghép cặp: ta không cần phải ghép mọi quan sát dựa trên các biến kiểm soát X, mà chỉ cần ghép chúng dựa trên biến duy nhất là điểm xu hướng e(X). Phương pháp này được gọi là ghép cặp điểm xu hướng.
psm = NearestNeighborMatch(replace=False, random_state=1)
df_ipwmatched = psm.match(data=df, treatment_col="nền_tối", score_cols=['pscore'])
Như nói ở trên, sau khi ghép cặp, ta chỉ cần đơn giản ước lượng bằng cách tính hiệu của kì vọng, và nhớ rằng các quan sát không độc lập và cần thận trọng khi suy luận.
smf.ols("số_giờ_đọc ~ nền_tối", data=df_ipwmatched)\
.fit(cov_type='cluster', cov_kwds={'groups': df_ipwmatched.index})\
.summary().tables[1]
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 18.5020 | 0.516 | 35.864 | 0.000 | 17.491 | 19.513 |
| nền_tối[T.True] | 1.0290 | 0.713 | 1.444 | 0.149 | -0.368 | 2.426 |
Tác động ước lượng của nền_tối dương, có ý nghĩa thống kê ở mức 1% và gần với giá trị thực 2!
Kết luận
Trong blog này, ta đã cùng xem xét phân tích điều kiện có thể tiến hành bằng nhiều cách. Ghép cặp trực tiếp ghép các cá nhân tương tự ở nhóm can thiệp với nhóm đối chứng. Bình quân gia quyền đơn giản gán các giá trị quyền số khác nhau cho từng quan sát theo xác suất chúng nhận can thiệp. Hồi quy thay vào đó gán quyền số cho các quan sát theo phương sai có điều kiện của tiếp nhận can thiệp. Hồi quy đặt quyền số lớn hơn cho các quan sát có thuộc tính phổ biến với cả nhóm can thiệp và đối chứng.
Các phương pháp này rất hữu dụng vì chúng hoặc cho phép ta ước lượng tác động nhân quả từ dữ liệu quan sát rất lớn hoặc điều chỉnh ước lượng thí nghiệm khi việc ngẫu nhiên hóa không hoàn hảo hoặc khi ta có mẫu nhỏ.
Cuối cùng, nếu bạn muốn tìm hiều thêm, tôi đề cử video bài giảng miễn phí về điểm xu hướng của Paul Goldsmith-Pinkham.
Tài liệu tham khảo
[1] P. Rosenbaum, D. Rubin, The central role of the propensity score in observational studies for causal effects (1983), Biometrika.
[2] G. Imbens, K. Hirano, G. Ridder, Efficient Estimation of Avertuổi Treatment Effects Using the Estimated Propensity Score (2003), Econometrica.
[3] J. Angrist, J. S. Pischke, Mostly harmless econometrics: An Empiricist’s Companion (2009), Princeton University Press.
Comments