Từ Tương Quan Tới Nhân Quả - Phần 2

SUY LUẬN NHÂN QUẢ CHO HỌC MÁY - KỲ 5

Bài viết này thuộc chuỗi bài viết về “Suy luận Nhân quả cho Học máy”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây

Để hiểu thêm kiến thức về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “Suy luận Nhân quả với Python” tại đây và “60 Giây Nhân quả với Python” tại đây

---

Trong phần trước, chúng ta đã tìm hiểu loại mô hình nhân quả trực tiếp làm phát sinh sự phụ thuộc giữa hai biến (mời bạn tìm đọc tại đây). Trong phần hai này chúng ta sẽ tìm hiểu thêm về hai cấu trúc nhân quả khác, cũng như cách thực hành một ví dụ đơn giản về Mô hình Cấu trúc nhân quả với Python.

(2) Nguyên nhân chung

Một tình huống thường gặp xảy ra khi một biến là nguyên nhân của nhiều biến khác. Nếu biến Z là nguyên nhân trực tiếp của cả biến X và Y thì Z được coi là nguyên nhân chung và chúng ta có cấu trúc ”dĩa”. Ví dụ, thất nghiệp có thể đồng thời gây ra tình trạng vỡ nợ và buộc người tiêu dùng giảm chi tiêu.

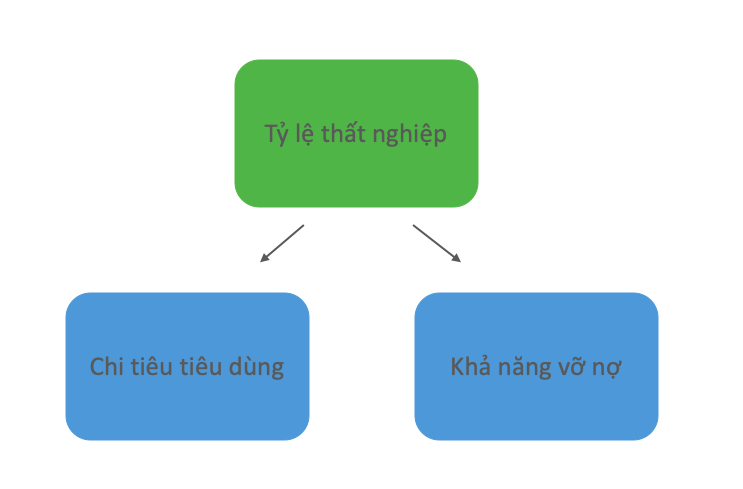
Cả chi tiêu tiêu dùng và khả năng vỡ nợ đều phụ thuộc vào tỷ lệ thất nghiệp nên chúng có mối tương quan với nhau. Một tỷ lệ thất nghiệp nhất định sẽ tạo ra một lượng chi tiêu tiêu dùng và khả năng vỡ nợ nhất định, và khi tỷ lệ thất nghiệp thay đổi, hai yếu tố còn lại cùng thay đổi theo. Do đó, trong phân phối đồng thời của Mô hình Nhân quả cấu trúc (SCM), hai biến phụ thuộc (chi tiêu tiêu dùng và khả năng vỡ nợ) sẽ có quan hệ thống kê với nhau.

Tuy nhiên, nếu ta đặt điều kiện về tỷ lệ thất nghiệp (ví dụ, bằng cách lọc dữ liệu tương ứng với tỷ lệ thất nghiệp ở một mức cố định, chúng ta sẽ thấy chi tiêu tiêu dùng và khả năng vỡ nợ độc lập với nhau. Ở đây, tỉ lệ thất nghiệp với vai trò nguyên nhân chung gây nhiễu lên mối quan hệ giữa chi tiêu và khả năng vỡ nợ. Chúng ta không thể tính toán chính xác mối quan hệ giữa chi tiêu và khả năng vỡ nợ nếu không tính đến tỷ lệ thất nghiệp.

Thật không may các yếu tố gây nhiễu thường khó hoặc không thể phát hiện chỉ từ dữ liệu quan sát. Thực tế nếu chỉ nhìn vào chi tiêu tiêu dùng và khả năng vỡ nợ, chúng ta có thể thấy phân phối đồng thời của 2 biến này trông như thể có mối quan hệ nhân quả trực tiếp. Trong trường hợp này, chúng ta nên coi biểu đồ nhân quả như là một cách mã hoá các giả thiết của ta về hệ thống mà ta đang nghiên cứu. Đến đây một câu hỏi tự nhiên sẽ phát sinh: Làm thế nào để nhận biết khi nào thì nên sử dụng loại biểu đồ nhân quả nào?

(3) Tác động chung

Một tình huống phổ biến khác xảy ra khi một tác động được gây ra bởi nhiều nguyên nhân trực tiếp. Một nút chịu tác động bởi nhiều nút “cha mẹ” được gọi là nút giao của các nút đó.

Nút giao phụ thuộc vào nhiều hơn một nguyên nhân. Trong ví dụ này, khả năng vỡ nợ phụ thuộc vào cả điểm tín dụng kinh doanh và số lần thế chấp tài sản (quyền giữ tài sản thuộc về một bên khác cho đến khi khoản nợ của bên đó được giải quyết).

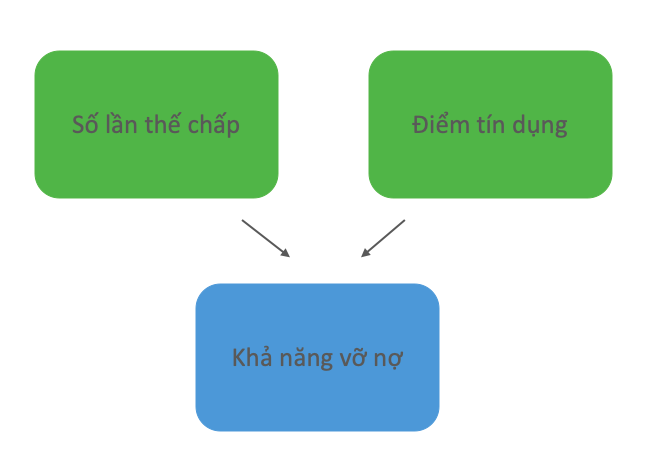
Nút giao khác với mô hình nhân quả trực tiếp và mô hình dĩa vì việc đặt điều kiện cho kết quả đối lập. Trước khi đặt bất kỳ điều kiện nào, điểm tín dụng kinh doanh và số lần thế chấp tài sản độc lập vô điều kiện. Không có biến nào là nguyên nhân chung cũng như không có mối quan hệ nhân quả trực tiếp nào giữa chúng, nên không tồn tại mối quan hệ thống kê. Tuy nhiên, nếu đặt điều kiện lên nút va chạm, chúng ta sẽ tạo ra sự phụ thuộc có điều kiện giữa điểm tín dụng kinh doanh và số lần thế chấp tài sản.

Điều này dường như không dễ tiếp nhận. Nhưng chúng ta có thể hiểu nó qua một thử nghiệm nhỏ. Khả năng vỡ nợ phụ thuộc vào cả điểm tín dụng kinh doanh và số lần thế chấp tài sản, vì vậy nếu một trong hai giá trị đó thay đổi, thì khả năng vỡ nợ sẽ thay đổi. Chúng ta cố định khả năng vỡ nợ (giả sử, chúng ta chỉ xem xét những trường hợp đã vỡ nợ). Bây giờ, nếu chúng ta tìm hiểu được điều gì đó về giá trị của điểm tín dụng kinh doanh, chúng ta cũng sẽ biết thêm đôi điều về số lần thế chấp tài sản. Cụ thể hơn, chỉ một số giá trị nhất định của số lần thế chấp tài sản mới tương ứng với giá trị đã sàng lọc của khả năng vỡ nợ và giá trị quan sát được của điểm tín dụng kinh doanh. Như vậy, đặt điều kiện lên một nút giao tạo ra một mối tương quan giả giữa các nút cha mẹ. Hay nói cách khác, đặt điều kiện lên một nút giao tạo ra thiên lệch chọn.

Mô hình Nhân quả cấu trúc với Python

Các biểu đồ nhân quả đơn giản đã được trình bày trên đây là một cách trực quan để hiểu về quan hệ nhân quả. Hơn nữa, chúng ta có thể thực hiện nhiều suy luận nhân quả (và ước lượng tác động nhân quả) với những biểu đồ này đơn giản bằng cách gán một giá trị cụ thể cho các biến có tác động nhân quả lên các biến khác. Biểu đồ nhân quả trong thực tế có thể rất lớn và có cấu trúc phức tạp.

Đương nhiên, có những cách khác để mã hoá thông tin. Với biểu đồ nhân quả, ta có thể dễ dàng tạo ra một biểu thức cho phân phối đồng thời của các biến: là tích của các phân phối xác suất có điều kiện cho từng nút theo các nút cha mẹ trực tiếp của nó. Trong trường hợp cấu trúc giao, \(x → z ← y\), hàm phân phối đồng thời là

\[p(x,y,z) = p(x) p(y) p(z\|x,y)\]

Xác suất có điều kiện \(p(z\|x,y)\) chính xác là hàm số ta thường ước lượng trong học có giám sát.

Nếu có thêm thông tin về hệ thống, ta có thể chuyển đổi biểu đồ nhân quả này thành một mô hình cấu trúc nhân quả toàn phần. Hãy cùng xem xét một ví dụ về SCM tương ứng với biểu đồ nhân quả sau:

from numpy.random import randn

def x():
  return -5 + randn()

def y():
  return 5 + randn()

def z(x, y):
  return x + y + randn()

def sample():
  x_ = x()
  y_ = y()
  z_ = z(x_, y_)
  return x_, y_, z_

Mỗi biến số được tạo lập bởi một biến nhiễu ngẫu nhiên độc lập bắt nguồn từ những yếu tố không được mô hình hoá bởi biểu đồ. Các phân phối này không nhất thiết phải giống nhau nhưng phải đáp ứng tính độc lập. Lưu ý rằng cấu trúc của biểu đồ mã hoá sự phụ thuộc giữa các biến. Giá trị của \(x\) và \(y\) độc lập, nhưng giá trị của \(z\) phụ thuộc vào cả hai. Mô hình đang xác định một quá trình tạo lập dữ liệu tổng quát vì chúng ta có thể lấy mẫu từ phân phối đồng thời bằng cách gọi hàm \(sample\). Lặp lại điều này nhiều lần cho phép ta lập biểu đồ phân phối đồng thời và thấy rằng \(x\) và \(y\) thực sự độc lập. Không có mối tương quan rõ ràng nào trong biểu đồ phân tán.

import random
random.seed(10)
x_sample, y_sample, z_sample = [], [], []
for i in range(20000):
    data = sample()
    x_0, y_0, z_0 = data[0], data[1], data[2]
    x_sample.append(x_0)
    y_sample.append(y_0)
    z_sample.append(z_0)
    
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('seaborn-white')

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(9,5))

kwargs = dict(histtype='stepfilled', alpha=0.3, bins=30)

ax1.hist(x_sample, **kwargs, label = 'x')
ax1.hist(y_sample, **kwargs, label = 'y')
ax1.hist(z_sample, **kwargs, label = 'z')
ax1.set_xlim([-10, 10])
ax1.set_ylim([0, 2500])
ax1.set_xlabel('giá trị', fontsize=12)
ax1.set_ylabel('số lượng mẫu', fontsize=12)
ax1.legend(loc='upper right')

ax2.scatter(x_sample, y_sample, alpha=0.3, )
ax2.set_xlim([-10, 0])
ax2.set_ylim([0, 10])
ax2.set_xlabel('x', fontsize=12)
ax2.set_ylabel('y', fontsize=12)
plt.show()

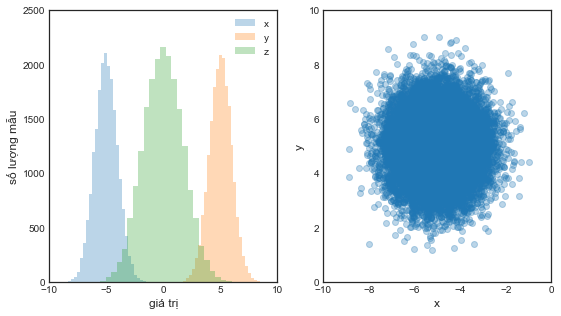
Bên trái: Biểu đồ tần suất của các phân phối quan sát của \(x, y\) và \(z\).

Bên phải: Biểu đồ phân tán của phân phối quan sát đồng thời của \(x\) và \(y\).

Vì \(x\) và \(y\) không có quan hệ nhân quả trực tiếp mà chỉ thông qua nút chung \(z\), nên chúng hoàn toàn không tương quan với nhau.

Bây giờ chúng ta đã có một mô hình với Python, chúng ta có thể quan sát tác động của thiên lệch chọn. Nếu chúng ta đặt điều kiện lên nút giao \(z\) lớn hơn một ngưỡng, ví dụ như \(z > 2.5\), mối quan hệ giữa \(x\) và \(y\) chuyển từ độc lập sang tương quan nghịch. Đây là một ví dụ đơn giản để hiểu về mô hình tác động chung với Python. Qua đó, ta đã thấy được hai biến nguyên nhân trực tiếp độc lập sẽ xuất hiện quan hệ tương quan nếu ta đặt điều kiện lên nút giao.

index_list = np.array(np.where(np.array(z_sample) > 2.5))
index_list = index_list.reshape(index_list.shape[1])
x_cutoff = [x_sample[i] for i in index_list]
y_cutoff = [y_sample[i] for i in index_list]
z_cutoff = [z_sample[i] for i in index_list]

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(9,5))

kwargs = dict(histtype='stepfilled', alpha=0.3, bins=30)

ax1.hist(x_cutoff, **kwargs, label = 'x')
ax1.hist(y_cutoff, **kwargs, label = 'y')
ax1.hist(z_cutoff, **kwargs, label = 'z')
ax1.set_xlim([-10, 10])
ax1.set_ylim([0, 500])
ax1.set_xlabel('giá trị', fontsize=12)
ax1.set_ylabel('số lượng mẫu', fontsize=12)
ax1.legend(loc='upper right')

ax2.scatter(x_cutoff, y_cutoff, alpha=0.3, )
ax2.plot(np.unique(x_cutoff), np.poly1d(np.polyfit(x_cutoff, y_cutoff, 1))(np.unique(x_cutoff)), 'tab:orange')
ax2.set_xlim([-10, 0])
ax2.set_ylim([0, 10])
ax2.set_xlabel('x', fontsize=12)
ax2.set_ylabel('y', fontsize=12)
plt.show()

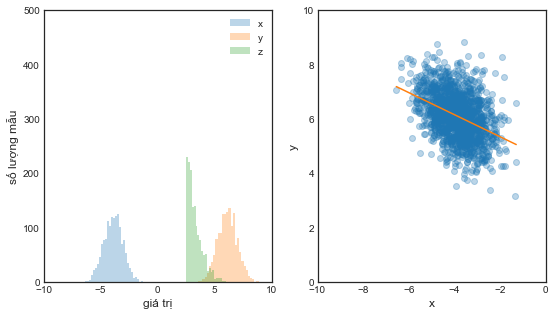
Bên trái: chúng ta điều chỉnh \(z > 2.5\) bằng cách lọc các mẫu (lưu ý sự thay đổi về cỡ mẫu), điều này thay đổi phân phối của \(x\) và \(y\), chúng đều dịch chuyển sang phải. Bên phải: Phân phối đồng thời có điều kiện của cả \(x\) và \(y\), với đường ước lượng tuyến tính thể hiện mối tương quan nghịch giữa hai biến.