Giới thiệu Suy luận Nhân quả

SUY LUẬN NHÂN QUẢ VỚI PYTHON - KỲ 1

Bài viết này thuộc chuỗi bài viết về “Suy luận Nhân quả với Python”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây

Để hiểu một cách trực quan về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “60 Giây Nhân quả” tại đây

Sao phải Quan tâm?

Khoa Học Dữ Liệu Không còn là Nó Trước đây (hoặc Nó của Ngày sau)

Chuyên gia dữ liệu được lăng xê là Nghề nghiệp Quyến rũ nhất Thế kỉ 21 bởi Harvard Business Review. Đây không phải là một diễn ngôn trống rỗng. Trong thập kỉ vừa qua, Chuyên Gia Dữ Liệu thực sự tỏa sáng. Các chuyên gia AI sở hữu mức lương không hề kém cạnh các siêu sao thể thao. Theo đuổi tiền tài và danh vọng, hàng trăm các chuyên gia trẻ lao đầu vào cuộc đua truy tìm kho báu cố giành danh hiệu chuyên gia dữ liệu sớm nhất. Ngành nghề mới như thể đang lên đồng. Một vài phương pháp giảng dạy tân tiến có thể giúp bạn trở thành một chuyên gia dữ liệu mà không phải nhìn dù chỉ một công thức toán học. Các chuyên gia tư vấn hứa hẹn triệu đô nếu công ty của bạn có thể hé mở tiềm năng dữ liệu. AI hoặc, ML, được gọi là nguồn điện mới và dữ liệu là mỏ dầu mới.

Trong khi ấy, chúng ta lãng quên các ngành khoa học xưa cũ vốn vẫn sử dụng dữ liệu từ trước đến nay. Xưa nay các chuyên gia kinh tế cố trả lời đâu là tác động thực sự của giáo dục đối với thu nhập. Các chuyên gia thống kê y sinh cố tìm hiểu liệu chất béo bão hòa có làm tăng nguy cơ nhồi máu cơ tim. Các chuyên gia tâm lý nghiên cứu liệu những lời xác nhận có làm hôn nhân hạnh phúc hơn. Thành thật mà nói, khoa học dữ liệu không phải là một ngành khoa học mới. Bạn chỉ biết nhiều hơn về nó gần đây vì lượng thông tin marketing khổng lồ từ truyền thông.

Sử dụng phép so sánh của Jim Collins, hãy nghĩ về việc bạn đang chế một cốc bia đá lạnh yêu thích. Nếu bạn làm đúng cách, phần lớn chiếc cốc sẽ đầy bia với một lớp bọt dầy phía trên. Chiếc cốc ấy thật giống khoa học dữ liệu.

1. Nó là bia. Nền tảng thống kê đã được chứng minh giá trị hàng trăm năm qua.
2. Nó là bọt. Những bong bóng được dựng trên nền kì vọng viển vông và sẽ dần tan biến.

Thứ bọt này có thể biến mất nhanh hơn bạn nghĩ. Tạp chí “The Economist” từng viết:

Những chuyên gia tư vấn từng dự đoán AI có tác động thay đổi thế giới cũng chính là những người tường thuật việc các nhà quản lý thực tế tại các công ty đang ngộ ra rằng AI rất khó triển khai, và cơn sốt đang nguội dần. Svetlana Sicular từ công ty nghiên cứu Gartner nói rằng năm 2020 có thể là năm AI đổ đèo, trong mô hình “Vòng đời Ảo vọng” nổi tiếng. Các nhà đầu tư sực tỉnh khi đang chạy theo đám đông: một khảo sát các startup AI tại châu Âu của MMC, một quỹ đầu tư mạo hiểm, cho thấy thực tế 40% không hề dùng AI chút nào.

Giữa cơn lên đồng ấy, chúng ta, các chuyên gia dữ liệu, nên làm gì. Trước tiên, nếu bạn khôn ngoan, bạn sẽ học cách phớt lờ lớp bọt. Cái mà ta muốn thưởng thức là bia. Toán và thống kê vốn hữu ích muôn đời và sẽ chẳng thể bỗng dưng thoái trào ở đây. Thêm vào đó, hãy học những gì khiến công việc của bạn hữu ích và giá trị, không phải những công cụ hào nhoáng chẳng biết để làm gì. Cuối cùng hãy nhớ rằng không thể đi ngang về tắt. Kiến thức về toán và thống kê giá trị chính vì chúng khó để học và dùng. Nếu mọi người đều có khả năng sử dụng, thì nguồn cung thừa mứa sẽ hạ giá trị của chúng. Vì thế, hãy khổ luyện và học chúng nhiều nhất có thể!

Trả lời những câu hỏi khác nhau

Vấn đề mà ML đang làm rất tốt là dự đoán. Ajay Agrawal, Joshua Gans và Avi Goldfarb viết trong cuốn sách “Cỗ máy Dự đoán”: “Làn sóng trí tuệ nhân tạo thực ra không mang đến cho chúng ta trí tuệ mà một phần thiết yếu của trí tuệ - khả năng phán đoán”. Chúng ta có thể tạo ra vô số điều kì diệu với “machine learning”. Yêu cầu duy nhất là chúng ta đặt vấn đề trong khuôn khổ dự đoán. Muốn dịch tiếng Anh sang tiếng Bồ Đào Nha? Hãy xây dựng mô hình ML giúp dự đoán câu văn tiếng Bồ Đào Nha cho mỗi câu tiếng Anh. Muốn nhận diện khuôn mặt? Hãy xây dựng mô hình ML giúp dự đoán sự hiện diện của một khuôn mặt trong một phần bức tranh. Muốn sản xuất ô tô tự lái? Hãy xây dựng mô hình ML giúp dự đoán phương hướng bánh lái và áp lực lên chân phanh và chân ga dựa vào các tấm hình ngoại cảnh ô tô.

Tuy nhiên ML không phải liều thuốc vạn năng. Nó rất kì diệu trong một khuôn khổ nhất định và thất bại nếu dữ liệu dùng để dự đoán sai lệch đôi chút với dữ liệu xây dựng mô hình mà nó đã quen thuộc. Một ví dụ khác trong cuốn sách “Cỗ máy Dự đoán”: “Trong nhiều ngành nghề, mức giá thấp tương quan với doanh số thấp. Ví dụ trong ngành khách sạn, giá thấp ngoài mùa du lịch và giá tăng cao khi nhu cầu đạt đỉnh điểm và các khách sạn kín phòng. Dựa vào dữ liệu, một mô hình dự đoán ngờ nghệch có thể đề xuất rằng việc tăng giá làm tăng mức độ phủ kín phòng.”

ML rất dở trong các vấn đề liên quan đến mối liên hệ ngược giữa nguyên nhân - kết quả. Chúng buộc chúng ta trả lời những câu hỏi “Nếu .. thì chuyện gì xảy ra”, mà các chuyên gia kinh tế gọi là các giả tưởng. Điều gì xảy ra nếu thay vì mức giá niêm yết này cho một mặt hàng, tôi niêm yết mức giá khác? Điều gì xảy ra nếu thay vì chế độ ăn ít béo, tôi theo chế độ ăn ít đường? Nếu bạn làm việc cho một ngân hàng cung cấp tín dụng, bạn sẽ phải tìm hiểu liệu việc thay đổi tập khách hàng sẽ thay đổi doanh số như thế nào? Hoặc nếu bạn làm việc cho một chính quyền địa phương , bạn có thể sẽ phải tìm hiểu làm thế nào để cải thiện hệ thống giáo dục. Liệu bạn có nên phát máy tính bảng cho mỗi đứa trẻ cho hợp thời đại kỉ nguyên trí tuệ số? Hoặc liệu có nên xây các thư viện theo kiểu truyền thống? Dù bạn làm ngành nghề nào thì bạn cũng sẽ phải đối mặt với những câu hỏi kiểu như “chiến dịch marketing này sẽ mang tới bao nhiêu khách hàng mới?”, “chương trình huấn luyện nhân viên này có làm tăng hiệu suất làm việc không?”. Đáng tiếc cho ML, trong các ngành nghề truyền thống, các loại câu hỏi này phổ biến hơn các câu hỏi về dự đoán. Để trả lời chúng, chúng ta không thể dựa vào các dự đoán dựa trên quan hệ tương quan.

Trả lời các câu hỏi kiểu này khó hơn mọi người tưởng. Ai đó có thể nói đi nói lại “Quan hệ tương quan không phải Quan hệ nhân quả”, “Quan hệ tương quan không phải Quan hệ nhân quả”. Nhưng thực tế để giải thích nó tường tận cần nhiều hơn thế. Phần dưới đây sẽ trình bày làm thể nào để quan hệ tương quan hé lộ quan hệ nhân quả.

Khi nào Quan hệ tương quan là Quan hệ nhân quả

Bằng trực giác, khá dễ hiểu tại sao quan hệ tương quan không phải quan hệ nhân quả. Nếu ai đó nói với bạn: trẻ học tốt hơn ở các trường phát máy tính bảng cho học sinh, bạn có thể phản biện rằng đó cũng là các trường giàu hơn. Vì thế họ có có điều kiện giảng dạy tốt hơn dù có phát máy tính bảng hay không. Vì thế chúng ta không thể kết luận rằng việc cung cấp máy tính bảng cho lớp học làm tăng kết quả học tập của trẻ. Chúng ta chỉ có thể nói rằng việc sử dụng máy tính bảng trong trường học tương quan với kết quả học tập cao.

import pandas as pd
import numpy as np
from scipy.special import expit
import seaborn as sns
from matplotlib import pyplot as plt
from matplotlib import style

style.use("fivethirtyeight")

np.random.seed(123)
n = 100
học_phí = np.random.normal(1000, 300, n).round()
máy_tính_bảng = np.random.binomial(1, expit((học_phí - học_phí.mean()) / học_phí.std())).astype(bool)
điểm_enem = np.random.normal(200 - 50 * máy_tính_bảng + 0.7 * học_phí, 200)
điểm_enem = (điểm_enem - điểm_enem.min()) / điểm_enem.max()
điểm_enem *= 1000

data = pd.DataFrame(dict(điểm_enem=điểm_enem, học_phí=học_phí, máy_tính_bảng=máy_tính_bảng))

plt.figure(figsize=(6,8))
sns.boxplot(y="điểm_enem", x="máy_tính_bảng", data=data).set_title(' Điểm ENEM theo việc trang bị Máy tính bảng trong Lớp học')
plt.show()

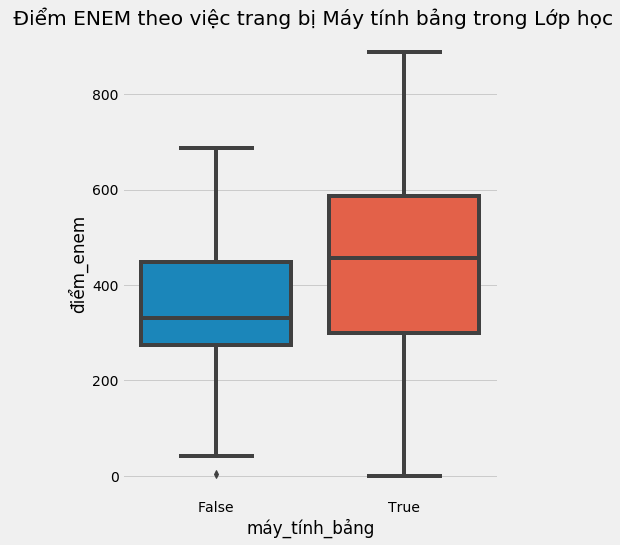
Để hiểu hơn vấn đề đơn giản này, hãy cùng bắt đầu với việc thiết lập một số kí hiệu. Đây là ngôn ngữ chung để nói về quan hệ nhân quả. Gọi \(T_i\) là lượng can thiệp đối với cá nhân i.

\[T_i=\begin{cases} 1 \ \text{nếu cá thể i tiếp nhận can thiệp}\\ 0 \ \text{nếu ngược lại}\\ \end{cases}\]

Can thiệp ở đây không nhất thiết là điều trị y tế hoặc bất cứ thứ gì liên quan đến lĩnh vực y tế. Thay vào đó, nó chỉ là một thuật ngữ chúng ta dùng để nói về một biện pháp/hành động/chương trình/sáng kiến mà chúng ta muốn tìm hiểu tính hiệu quả của nó. Trong trường hợp này, can thiệp là việc phát máy tính bảng cho học sinh.

Gọi biến \(Y_i\) là kết quả quan sát cho cá thể i.

\[Y_i\]

Kết quả là biến số chúng ta quan tâm. Chúng ta muốn biết liệu can thiệp có ảnh hưởng đến kết quả hay không.

Đây là điều thú vị. Thách thức cơ bản của suy luận nhân quả là chúng ta không bao giờ có thể quan sát cùng một cá thể đồng thời tiếp nhận hoặc không tiếp nhận can thiệp. Giống như việc chúng ta đi đến ngã rẽ và chỉ có thể biết điều gì chờ đón phía trước nếu chúng ta chọn đi một trong 2 con đường. Hãy nghĩ về thơ của Robert Frost [Con đường chưa đi/The road not taken]

Con đường chia hai ngả giữa rừng thu Nhưng than ôi, đành phải theo một lối Tôi làm kẻ lữ hành phân vân mãi Đưa mắt nhìn xuống lối chạy về xa Tới khúc cong khuất sau lùm cây bụi.

Tóm lại, chúng ta sẽ nói rất nhiều về các kết quả tiềm năng. Chúng tiềm năng vì chưa thực sự diễn ra. Thay vào đó, chúng cho ta biết điều gì có thể xảy đến nếu có can thiệp. Đôi khi chúng ta gọi kết quả tiềm năng diễn ra là hiện thực và kết quả tiềm năng không diễn ra là giả tưởng.

Chúng ta dùng chỉ số dưới để kí hiệu:

\(Y_{0i}\) là kết quả tiềm năng của cá thể i không được can thiệp (đối chứng).

\(Y_{1i}\) là kết quả tiềm năng của cùng cá thể i khi có can thiệp.

Lưu ý đôi khi chúng ta nhìn thấy các kết quả tiềm năng được kí hiệu dưới dạng hàm số \(Y_i(t)\). \(Y_{0i}\) có thể là \(Y_i(0)\) và \(Y_{1i}\) có thể là \(Y_i(1)\). Ở đây chúng ta sẽ chủ yếu dùng chỉ số dưới để kí hiệu.

Trong ví dụ máy tính bảng của chúng ta, \(Y_{1i}\) là kết quả học tập của học sinh i nếu được phát máy tính bảng dùng trong lớp học. Bây giờ, nếu học sinh i được phát máy tính bảng, chúng ta quan sát thấy \(Y_{1i}\). Nếu không, \(Y_{1i}\) vẫn tồn tại trên lí thuyết nhưng chúng ta không thể quan sát. Trong trường hợp này nó là một kết quả tiềm năng (giả tưởng).

Với kết quả tiềm năng, chúng ta có thể định nghĩa hiệu ứng can thiệp cá thể:

\(Y_{1i} - Y_{0i}\)

Tất nhiên, do thách thức cơ bản của suy luận nhân quả, chúng ta không bao giờ biết được hiệu ứng can thiệp cá thể vì chúng ta chỉ có thể quan sát được 1 trong 2 kết quả tiềm năng. Vì vậy, hãy tập trung ước lượng một đại lượng đơn giản hơn: tác động can thiệp trung bình (Average Treatment Effect - ATE). Đại lượng này được định nghĩa như sau:

\(ATE = E[Y_1 - Y_0]\)

Trong đó E[…] là giá trị kì vọng. Một đại lượng dễ ước tính hơn nữa là tác động can thiệp trung bình trên nhóm đươc can thiệp (Average Treatment Effect on the Treated - ATET):

\(ATET = E[Y_1 - Y_0 | T=1]\)

Chúng ta biết rằng sẽ không bao giờ có thể quan sát được cả 2 kết quả tiềm năng, nhưng để dễ hiểu hơn, hãy tạm giả thiết là ta có thể. Giả sử chúng ta thu thập dữ liệu cho 4 trường học. Chúng ta quan sát được từng trường có phát máy tính bảng cho học sinh hay không và kết quả học tập của học sinh. Ở đây việc phát máy tính bảng là can thiệp, vì thế \(T=1\) tương ứng với việc phát máy tính bảng cho học sinh. \(Y\) là điểm số.

pd.DataFrame(dict(
    i= [1,2,3,4],
    y0=[500,600,800,700],
    y1=[450,600,600,750],
    t= [0,0,1,1],
    y= [500,600,600,750],
    te=[-50,0,-200,50],
))

	i	y0	y1	t	y	te
0	1	500	450	0	500	-50
1	2	600	600	0	600	0
2	3	800	600	1	600	-200
3	4	700	750	1	750	50

\(ATE\) ở đây là trung bình cộng của cột cuối cùng (tác động can thiệp):

\(ATE=(-50 + 0 - 200 + 50)/4 = -50\)

\(ATET\) ở đây là trung bình cộng của cột cuối cùng khi mà \(T=1\):

\(ATET=(- 200 + 50)/2 = -75\)

Điều này nghĩa là với các trường nhận can thiệp, tính trung bình, máy tính bảng làm giảm kết quả học tập của học sinh 75 điểm. Tất nhiên chúng ta không bao giờ biết rõ như thế. Bảng số liệu trên đây thực tế trông giống thế này (NaN là các giá trị chưa biết):

pd.DataFrame(dict(
    i= [1,2,3,4],
    y0=[500,600,np.nan,np.nan],
    y1=[np.nan,np.nan,600,750],
    t= [0,0,1,1],
    y= [500,600,600,750],
    te=[np.nan,np.nan,np.nan,np.nan],
))

	i	y0	y1	t	y	te
0	1	500.0	NaN	0	500	NaN
1	2	600.0	NaN	0	600	NaN
2	3	NaN	600.0	1	600	NaN
3	4	NaN	750.0	1	750	NaN

Thiên lệch

Thiên lệch là nguyên nhân khiến quan hệ tương quan khác với quan hệ nhân quả. May mắn là nó khá dễ hiểu bằng trực giác thông thường. Quay trở lại với ví dụ máy tính bảng trong lớp học của chúng ta. Nếu ai đó khẳng định rằng học sinh học tập tốt hơn tại các trường phát máy tính bảng; chúng ta có thể phản biện rằng các trường đó có điều kiện giảng dạy tốt hơn dù có phát máy tính bảng hay không. Các trường này nhiều khả năng giàu hơn các trường khác và vì thế trả lương giáo viên cao hơn, trang bị phòng học tốt hơn ,… Nói cách khác, trường học được can thiệp (phát máy tính bảng) không thể so sánh với các trường đối chứng.

Sử dụng kí hiệu, kết quả tiềm năng \(Y_0\) của trường được can thiệp khác với \(Y_0\) của trường đối chứng. Lưu ý \(Y_0\) của trường được can thiệp là giả tưởng. Chúng ta không quan sát được nó, nhưng chúng ta có thể suy luận về nó. Trong trường hợp cụ thể này, chúng ta có thể đi xa hơn và khái quát cách thế giới vận hành. Chúng ta có thể nói rằng \(Y_0\) của trường được can thiệp lớn hơn \(Y_0\) của trường đối chứng. Vì trường đủ tiền phát máy tính bảng cho học sinh thì cũng đủ tiền để trang trải các điều kiện vật chất khác giúp trẻ đạt điểm cao hơn. Hãy dừng lại ở đây một chút. Phải mất chút thời gian để quen với cách nói về các kết quả tiềm năng. Hãy thử đọc lại đoạn văn này để chắc chắn rằng bạn thực sự hiểu nó.

Bây giờ chúng ra có thể chứng minh bằng toán học tại sao quan hệ tương quan không phải quan hệ nhân quả. Quan hệ tương quan được đo bởi \(E[Y|T=1] - E[Y|T=0]\). Trong ví dụ của chúng ta, nó là hiệu giữa điểm thi trung bình của các trường phát máy tính bảng và điểm thi trung bình của các trường không phát máy tính bảng. Trong khi đó, quan hệ nhân quả được đo bởi \(E[Y_1 - Y_0]\).

Để biết chúng liên quan đến nhau như thế nào, hãy dùng công thức tính quan hệ tương quan và thay các kết quả quan sát bằng các kết quả tiềm năng. Với các trường được can thiệp, kết quả quan sát là \(Y_1\). Với các trường đối chứng, kết quả quan sát là \(Y_0\).

\[E[Y|T=1] - E[Y|T=0] = E[Y_1|T=1] - E[Y_0|T=0]\]

Bây giờ hãy cộng rồi trừ kết quả giả tưởng \(E[Y_0|T=1]\). Nó cho ta biết điều gì xảy ra với kết quả của các trường được can thiệp nếu chúng không nhận can thiệp.

\[E[Y|T=1] - E[Y|T=0] =\] \[E[Y_1|T=1] - E[Y_0|T=0] + E[Y_0|T=1] - E[Y_0|T=1]\]

Cuối cùng, chúng ta sắp xếp lại và nhóm các kì vọng và thu được:

\[E[Y|T=1] - E[Y|T=0] = \underbrace{E[Y_1 - Y_0|T=1]}_{ATET}\] \[+ \underbrace{\{ E[Y_0|T=1] - E[Y_0|T=0] \}}_{THIÊN LỆCH}\]

Công thức toán học đơn giản này có thể giúp ta giải quyết các vấn đề liên quan đến các câu hỏi về nhân quả. Tôi không thể nhấn mạnh hết việc hiểu ngọn ngành công thức này quan trọng đến nhường nào. Nếu bạn bị ép xăm một thứ gì đó lên cánh tay, phương trình này có thể là một lựa chọn tốt. Nó là một thứ gì đó cần giữ chặt lấy và cần thực sự hiểu, giống như một khẩu quyết có thể diễn giải theo hàng trăm cách khác nhau. Thực tế, hãy xem xét kĩ lưỡng hơn và tìm hiểu một vài hàm ý của nó.

Trước hết, phương trình này giải thích tại sao quan hệ tương quan không phải quan hệ nhân quả. Chúng ta có thể thấy quan hệ tương quan bao gồm tác động can thiệp trên nhóm được can thiệp cộng với phần thiên lệch. Thiên lệch được tính bằng khác biệt giữa nhóm được can thiệp và nhóm đối chứng trước khi có can thiệp, nếu tạm giả thiết cả 2 nhóm đều chưa từng nhận can thiệp. Bây giờ ta có thể nói chính xác vì sao ta nghi ngờ nếu ai đó nói rằng việc dùng máy tính bảng trong lớp học tăng cường kết quả học tập. Chúng ta cho rằng, trong trường hợp này, \(E[Y_0|T=0] < E[Y_0|T=1]\), nghĩa là, các trường có tiền để phát máy tính bảng vốn dĩ hoạt động tốt hơn các trường khác, dù có can thiệp phát máy tính bảng hay không.

Tại sao lại có điều này? Chúng ta sẽ nói kĩ hơn khi về vấn đề này khi đề cập đến nhiễu (trong các bài tới), nhưng bây giờ bạn có thể nghĩ về việc thiên lệch xảy ra do nhiều yếu tố chúng ta không thể kiếm soát nhưng tác động đến can thiệp. Kết quả là các trường được can thiệp và đối chứng không chỉ khác nhau về việc phát máy tính bảng. Chúng cũng có thể khác biệt về học phí, địa điểm, giáo viên … Để chúng ta có thể nói rằng việc dùng máy tính bảng trong lớp học làm tăng kết quả học tập, chúng ta cần đảm bảo các trường học theo đuổi và không theo đuổi chính sách này tương tự nhau về mặt bằng chung.

plt.figure(figsize=(10,6))
sns.scatterplot(x="học_phí", y="điểm_enem", hue="máy_tính_bảng", data=data, s=70).set_title('Điểm ENEM theo Học phí')
plt.show()

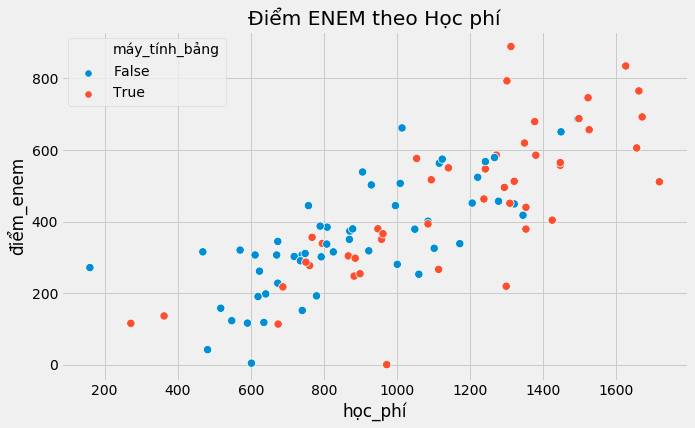
Chúng ta cũng có thể nêu điều kiện cần để quan hệ tương quan đồng thời là quan hệ nhân quả. Nếu \(E[Y_0|T=0] = E[Y_0|T=1]\), thì, quan hệ tương quan LÀ QUAN HỆ NHÂN QUẢ! Để hiểu điều này không chỉ cần ghi nhớ công thức. Có một lập luận khá trực quan ở đây. Nói rằng \(E[Y_0|T=0] = E[Y_0|T=1]\) nghĩa là nói rằng nhóm được can thiệp và nhóm đối chứng khá tương đồng khi không tính đến can thiệp. Hoặc, trong trường hợp giả thiết nhóm được can thiệp chưa được can thiệp, nếu ta có thể quan sát \(Y_0\), thì kết quả của nó phải tương tự như nhóm đối chứng. Về mặt toán học, phần thiên lệch bị giản ước.

\[E[Y|T=1] - E[Y|T=0] = E[Y_1 - Y_0|T=1]\]

Và nếu nhóm được can thiệp và nhóm đối chứng chỉ khác nhau ở can thiệp, tức là \(E[Y_0|T=0] = E[Y_0|T=1]\), ta có:

\[\begin{align} E[Y_1 - Y_0|T=1] &= E[Y_1|T=1] - E[Y_0|T=1] \\\\ &= E[Y_1|T=1] - E[Y_0|T=0] \\\\ &= E[Y|T=1] - E[Y|T=0] \end{align}\]

Vì thế trong trường hợp này, hiệu của các giá trị trung bình LÀ tác động nhân quả:

\[E[Y|T=1] - E[Y|T=0] = ATE = ATET\]

Điều này khá quan trọng, nên chúng ta hãy nhắc lại bằng một biểu đồ thú vị. Nếu chúng ta chỉ đơn thuần so sánh giá trị trung bình giữa nhóm được can thiệp và đối chứng, chúng ta thu được đồ thị sau (các chấm xanh không được nhận can thiệp, phát máy tính bảng):

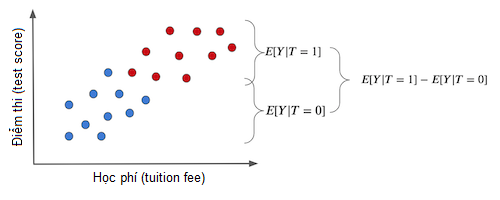
Lưu ý sự khác biệt trong kết quả giữa hai nhóm được tạo nên bởi 2 nguyên nhân:

1. Tác động can thiệp. Sự gia tăng điểm số thuần tuý do phát máy tính bảng cho học sinh.
2. Các khác biệt khác giữa nhóm được can thiệp và đối chứng KHÔNG được tạo ra bởi bản thân can thiệp.

Trong trường hợp này, nhóm được can thiệp và đối chứng khác nhau ở chỗ nhóm được can thiệp có học phí cao hơn hẳn. Một số khác biệt trong kết quả thi có thể do tác động tích cực của học phí cao với chất lượng giáo dục.

Chúng ta chỉ có thể biết được tác động thực sự của can thiệp nếu ta có quyền lực siêu nhiên quan sát được kết quả tiềm năng, giống như đồ thị bên trái dưới đây. Hiệu ứng can thiệp cá thể là hiệu giữa kết quả của mỗi cá nhân và kết quả lý thuyết của cùng cá nhân đó nếu thay đổi việc phân bổ can thiệp. Chúng là các kết quả giả tưởng và được biểu diễn bằng màu nhạt hơn.

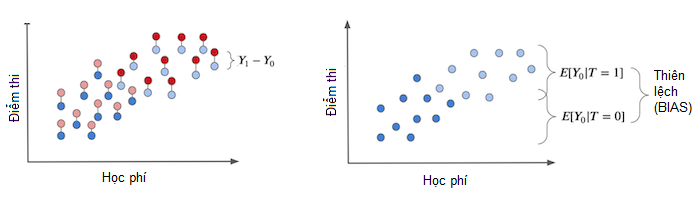
Ở đồ thị bên trái, ta biểu diễn thiên lệch được nhắc đến ở phần trước. Chúng ta thu được thiên lệch nếu chúng ta không chỉ định can thiệp cho bất kì ai. Trong trường hợp này, chúng ta chỉ còn kết quả tiềm năng \(Y_0\). Sau đó, ta theo dõi xem nhóm được can thiệp và đối chứng khác nhau như thế nào. Nếu chúng khác biệt, nhân tố nào đó ngoài can thiệp gây ra khác biệt giữa 2 nhóm. Nhân tố nào đó ở đây là nguyên nhân thiên lệch và gây nhiễu tác động can thiệp trong thực tế.

Bây giờ, hãy so sánh nó với tình huống giả tưởng rằng không có thiên lệch. Giả sử máy tính bảng được phát ngẫu nhiên tại các trường học. Trong các tình huống này, các trường giàu và trường nghèo đều nhận được can thiệp với xác suất như nhau. Can thiệp sẽ phân bổ đồng đều theo học phí.

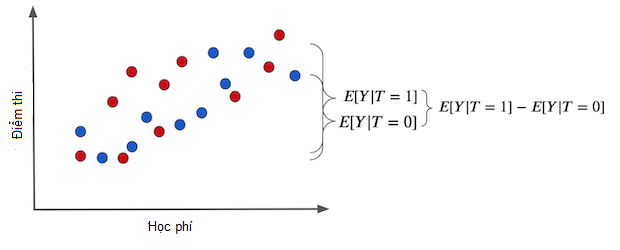
Trong trường hợp này, hiệu giữa kết quả của nhóm được can thiệp và đối chứng LÀ tác động nhân quả trung bình. Điều này xảy ra và không có nguyên nhân nào khác gây ra khác biệt giữa nhóm được can thiệp và đối chứng ngoài bản thân can thiệp. Vì thế mọi sự khác biệt đều có thể gán cho can thiệp. Nói cách khác là không có thiên lệch.

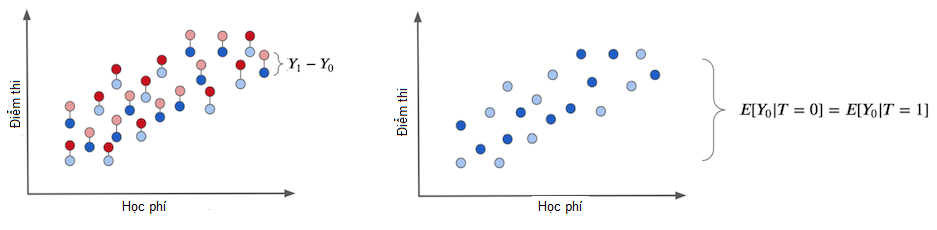
Nếu chúng ta sắp xếp để không ai được nhận can thiệp, và vì thế chúng ta chỉ quan sát được các \(Y_0\), chúng ta sẽ không thấy khác biệt giữa nhóm được can thiệp và đối chứng. Đây là mấu chốt của suy luận nhân quả. Tìm kiếm phương pháp thông minh để loại bỏ thiên lệch rồi từ đó quy kết mọi khác biệt giữa nhóm được can thiệp và đối chứng là do tác động can thiệp trung bình.

Đây là nhiệm vụ “khủng” của suy luận nhân quả. Nó đòi hỏi những phương thức thông mình để loại bỏ thiên lệch, làm cho các đối tượng nhận can thiệp và đối chứng tương đương và từ đó mọi khác biệt giữa chúng có thể gán cho tác động can thiệp trung bình. Mục đích sau cùng của suy luận nhân quả là khám phá cách thế giới vận hành, loại bỏ ảo giác và cách diễn giải sai lệch. Và bây giờ chúng ta hiểu điều này, chúng ta có thể tiến tới học cách phương pháp quyền lực giúp loại bỏ thiên lệch, vũ khí của những chiến binh Quả cảm Chân chính giúp xác định tác động nhân quả.

Ý tưởng chủ đạo

Trên đây chúng ta đã nhận thấy quan hệ tương quan không phải quan hệ nhân quả. Quan trọng hơn, chúng ta thấy rõ tại sao không phải vậy và làm thế nào để quan hệ tương quan trở thành quan hệ nhân quả. Chúng ta cũng đã tìm hiểu công thức kết quả tiềm năng như là một phương pháp để gói gọn vấn đề suy luận nhân quả. Cùng với đó, chúng ta tìm hiểu thống kê trong 2 tình huống hiện thực loại trừ nhau: có và không có can thiệp. Đáng tiếc là chúng ta chỉ có thể quan sát và đo lường 1 trong 2 tình huống đó, và đây là thách thức cơ bản của suy luận nhân quả.

Trong các bài tới, chúng ta sẽ tìm hiểu một số kĩ thuật cơ bản để ước lượng tác động nhân quả, bắt đầu từ tiêu chuẩn vàng nhờ vào thử nghiệm ngẫu nhiên. Tôi cũng sẽ tổng kết một số khái niệm thống kê cần dùng. Tôi kết thúc bài viết này với một cuộc thoại thường được trích dẫn trong các lớp học suy luận nhân quả từ series phim Kungfu:

‘Điều gì xảy đến với mỗi đời người đều đã được định sẵn. Ai bước qua cuộc đời này cũng đều theo số phận an bài mà thôi.’ Caine

‘Đúng vậy, nhưng mỗi người lại toàn quyền sống theo cách mình chọn lựa. Tưởng chừng mâu thuẫn, nhưng cả hai đều là chân lý.’ Trưởng lão

Tài liệu tham khảo

Tôi muốn dành loạt bài viết này để vinh danh Joshua Angrist, Alberto Abadie and Christopher Walters vì khóa học Kinh tế lượng tuyệt cú mèo của họ. Phần lớn ý tưởng trong loạt bài này được lấy từ các bài giảng của họ được tổ chức bởi Hiệp hội Kinh tế Mĩ. Theo dõi các bài giảng này là những gì tôi làm trong suốt năm 2020 khó nhằn.

• Kinh tế lượng với dữ liệu chéo
• Luyện chưởng Kinh tế lượng Gần như Vô hại

Tôi cũng muốn giới thiệu cuốn sách lý thú của Angrist. Chúng cho tôi thấy Kinh tế lượng, hoặc ‘Lượng theo cách họ gọi không chỉ vô cùng hữu ích mà còn rất vui.

• Kinh tế lượng Gần như Vô hại
• Luyện chưởng ‘Lượng’

Tài liệu tham khảo cuối cùng của tôi là cuốn sách của Miguel Hernan and Jamie Robins. Nó là người bạn đồng hành tin cậy với tôi khi trả lời những câu hỏi nhân quả khó nhằn.

• Sách Suy Luận Nhân Quả

Phép so sánh cốc bia trong bài này được lấy từ Đầu tư Chứng khoán, viết bởi JL Colins. Đây là loạt bài phải đọc cho bất kì ai muốn đầu tư hiệu quả.

Bảng Từ Viết tắt

Viết tắt	Tiếng Anh	Tiếng Việt
AI	Artificial Intelligence	Trí tuệ Nhân tạo
ATET	Average Treatment Effect on the Treated	Tác động Can thiệp Trung bình trên Nhóm được Can thiệp
ML	Machine Learning	Học Máy

Bảng Thuật ngữ

Thuật ngữ	Tiếng Anh
chuyên gia dữ liệu	data scientist
dự đoán	predict, prediction
giả tưởng	counterfactual
hiện thực	factual
hiệu ứng can thiệp cá thể	individual treatment effect
khoa học dữ liệu	data science
kinh tế lượng	econometrics
kết quả	outcome
kết quả giả tưởng	counterfactual outcome
kết quả quan sát	observed outcome
kết quả tiềm năng	potential outcome
nhiễu	confounding
nhóm được can thiệp	treatment group, test group
nhóm đối chứng	control group, untreated group
phần thiên lệch	bias term
quan hệ nhân quả	causality, causation, causal relationship
quan hệ tương quan	association, correlation
quan sát	observe, observation
suy luận nhân quả	causal inference, causal reasoning
thiên lệch	bias
thử nghiệm ngẫu nhiên	randomised trial
trí tuệ nhân tạo	artificial intelligence
tác động can thiệp	treatment effect, treatment impact
tác động can thiệp trung bình	average treatment effect
tác động can thiệp trung bình trên nhóm đươc can thiệp	average treatment effect on the treated
tác động can thiệp trên nhóm được can thiệp	treatment effect on the treated
tác động nhân quả trung bình	average causal effect
được can thiệp	treated
đối chứng	untreated, non-treated