Mô hình Biểu đồ Nhân quả
SUY LUẬN NHÂN QUẢ VỚI PYTHON - KỲ 4
Bài viết này thuộc chuỗi bài viết về “Suy luận Nhân quả với Python”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây
Để hiểu một cách trực quan về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “60 Giây Nhân quả” tại đây
Đôi điều về Quan hệ nhân quả
Một giả thiết tối thiểu chúng ta cần đặt ra khi thực hiện suy luận nhân quả là can thiệp độc lập có điều kiện với các kết quả tiềm năng.
\[(Y_0, Y_1) \perp T | X\]Điều này nghĩa là chúng ta có thể đo lường tác động của một mình sự can thiệp lên kết quả, mà không có sự can dự của bất kỳ biến nào khác. Một ví dụ điển hình là tác dụng của thuốc lên người bệnh. Nếu chỉ những bệnh nhân mắc bệnh nặng mới được dùng thuốc thì việc dùng thuốc có vẻ như làm suy giảm sức khoẻ của người bệnh. Đó là vì mức độ nghiêm trọng của bệnh và tác dụng của thuốc chưa được phân tích một cách tách bạch. Tuy nhiên nếu chúng ta chia bệnh nhân ra thành nhóm ca bệnh nghiêm trọng và nhóm ca bệnh không nghiêm trọng, sau đó phân tích tác dụng của thuốc lên từng nhóm, chúng ta sẽ có một cái nhìn rõ nét hơn về tác dụng thật sự của thuốc. Chúng ta có thể gọi việc chia tổng thể theo những đặc điểm của nó là kiểm soát hay là đặt điều kiện lên X. Đặt điều kiện lên các ca bệnh nghiêm trọng, cơ chế can thiệp trở nên ngẫu nhiên. Những bệnh nhân thuộc nhóm ca bệnh nghiêm trọng có thể hoặc không được dùng thuốc hoàn toàn là do ngẫu nhiên, chứ không phải do mức độ nghiêm trọng của bệnh như trước, bởi tất cả các ca bệnh này đều được xếp chung vào một mức độ nghiêm trọng. Và nếu sự can thiệp được chỉ định như thể ngẫu nhiên trong các nhóm, sự can thiệp trở nên độc lập có điều kiện với các kết quả tiềm năng.
Độc lập và độc lập có điều kiện là những khái niệm trung tâm trong suy luận nhân quả. Tuy vậy, để nắm bắt những khái niệm này không phải là một nhiệm vụ đơn giản. Để giải quyết điều này, chúng ta sử dụng cấu trúc của mô hình biểu đồ nhân quả. Mô hình biểu đồ nhân quả đưa ra một phương pháp biểu thị cách thức hoạt động của quan hệ nhân quả xét theo khía cạnh cái gì chi phối cái gì. Như chúng ta sẽ thấy ở phần tiếp theo, đây là một cách thức hiệu quả để suy ngẫm về quan hệ nhân quả và nắm rõ những biến nào chúng ta nên đặt điều kiện lên nhằm tạo ra những kết quả tiềm năng độc lập với sự can thiệp.
Một mô hình biểu đồ có thể được biểu diễn như sau
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
import graphviz as gr
from matplotlib import style
import seaborn as sns
from matplotlib import pyplot as plt
style.use("fivethirtyeight")
g = gr.Digraph()
g.edge("Z", "X")
g.edge("U", "X")
g.edge("U", "Y")
g.edge("thuốc", "khả năng sống")
g.edge("mức độ nghiêm trọng", "khả năng sống")
g.edge("mức độ nghiêm trọng", "thuốc")
g
Mỗi đỉnh là một biến ngẫu nhiên. Chúng ta sử dụng mũi tên, hoặc cạnh để biểu hiện một biến chi phối biến khác. Trong mô hình biểu đồ thứ nhất, chúng ta khẳng định rằng Z chi phối X, và U chi phối X và Y. Để cung cấp một ví dụ cụ thể hơn, chúng ta có thể biểu thị tác dụng của thuốc lên khả năng sống của bệnh nhân như mô hình biểu đồ thứ hai. “Mức độ nghiêm trọng” chi phối “thuốc” và “khả năng sống”, và “thuốc” cũng chi phối “khả năng sống”. Như chúng ta thấy, mô hình biểu đồ nhân quả giúp những suy luận về quan hệ nhân quả trở nên rõ ràng hơn bởi nó biểu hiện một cách trực quan quan điểm của chúng ta về cách mà thế giới vận hành.
Học nhanh về Mô hình biểu đồ
Bạn có thể tham khảo một khoá học dài hạn tại đây. Tuy nhiên, để phục vụ cho mục tiêu của chương này, chúng ta cần phải hiểu rõ những giả thiết về độc lập và độc lập có điều kiện mà mô hình biểu đồ yêu cầu. Chúng ta sẽ thấy sự độc lập xuyên suốt mô hình biểu đồ như thể dòng nước chảy qua sông qua suối. Chúng ta có thể ngăn chặn hoặc khai thông “dòng chảy” này tuỳ thuộc vào việc chúng ta xử lý các biến trong đó như thế nào. Để hiểu rõ hơn, hãy cùng xem xét một số cấu trúc và ví dụ phổ biến của mô hình biểu đồ. Chúng có thể khá đơn giản, nhưng lại là những nền tảng cần thiết để hiểu thấu đáo về độc lập và độc lập có điều kiện trong mô hình biểu đồ.
Trước tiên, hãy nhìn vào một biểu đồ vô cùng đơn giản. A dẫn đến B, B dẫn đến C. Hay X dẫn đến Y, Y dẫn đến Z.
g = gr.Digraph()
g.edge("A", "C")
g.edge("C", "B")
g.edge("X", "Y")
g.edge("Y", "Z")
g.node("Y", "Y", color="red")
g.edge("hiểu biết về nhân quả", "giải quyết vấn đề")
g.edge("giải quyết vấn đề", "thăng tiến")
g
Trong biểu đồ thứ nhất, sự phụ thuộc thể hiện qua hướng các mũi tên. Cụ thể hơn, giả sử rằng việc hiểu biết về suy luận nhân quả là cách duy nhất giải quyết các vấn đề trong kinh doanh, và giải quyết các vấn đề này là cách duy nhất để thăng tiến trong công việc. Chúng ta có thể nói rằng sự thăng tiến phụ thuộc vào hiểu biết về nhân quả. Càng có nhiều hiểu biết về quan hệ nhân quả thì cơ hội thăng tiến càng lớn. Lưu ý rằng sự phụ thuộc ở đây có tính đối xứng mặc dù không dễ nhận ra bằng trực giác. Cụ thể, khả năng thăng tiến của bạn càng cao thì khả năng bạn có hiểu biết về nhân quả càng lớn, nếu không thì sẽ rất khó để bạn được đề bạt.
Giả sử ta đặt điều kiện lên biến trung gian. Trong trường hợp này, sự phụ thuộc bị chặn lại. Vì vậy, X và Z độc lập với Y cho trước. Quay lại ví dụ trên, nếu tôi biết bạn là một người có kỹ năng giải quyết vấn đề tốt, thì việc biết rằng bạn có hiểu suy luận nhân quả không đưa ra thêm bất cứ thông tin nào về cơ hội thăng tiến của bạn trong công việc. Điều này có thể được biểu diễn một cách toán học như sau
\[E[Thăng \ tiến\|Giải \ quyết \ vấn \ đề, Hiểu \ biết \ nhân \ quả]\] \[=E[Thăng \ tiến\|Giải \ quyết \ vấn \ đề]\]Điều ngược lại cũng đúng, một khi tôi biết bạn có kỹ năng giải quyết vấn đề tốt, thì việc biết về sự thăng tiến của bạn trong công việc cũng không cung cấp cho tôi thêm thông tin gì hơn về việc bạn có hiểu biết về nhân quả hay không.
Theo nguyên tắc chung, sự phụ thuộc trên đường đi trực tiếp từ A tới B bị chặn khi chúng ta đặt đặt điều kiện lên biến trung gian C. Hoặc,
\[A \not\!\perp\!\!\!\perp B\]và
\[A \!\perp\!\!\!\perp B | C\]Hãy cùng xem xét một mẫu hình đinh ba trong biểu đồ. Trong trường hợp này, một biến đồng thời chi phối hai biến khác dưới biểu đồ. Hai biến này phụ thuộc lẫn nhau theo chiều ngược mũi tên và chúng ta có đường đi cửa sau. Chúng ta có thể đóng đường đi cửa sau và ngăn chặn sự phụ thuộc bằng cách đặt điều kiện lên nguyên nhân chung.
g = gr.Digraph()
g.edge("C", "A")
g.edge("C", "B")
g.edge("X", "Y")
g.edge("X", "Z")
g.node("X", "X", color="red")
g.edge("thống kê", "suy luận nhân quả")
g.edge("thống kê", "học máy")
g
Ví dụ, giả sử kiến thức về thống kê là nền tảng để bạn biết nhiều hơn về suy luận nhân quả và học máy. Nếu tôi không biết trình độ kiến thức thống kê của bạn tới đâu thì việc biết bạn giỏi về suy luận nhân quả khiến tôi nghĩ rằng bạn nhiều khả năng cũng giỏi về học máy. Đó là bởi vì, ngay cả khi tôi không biết trình độ kiến thức thống kê của bạn, tôi vẫn có thể suy ra từ kiến thức về suy luận nhân quả của bạn: nếu bạn giỏi về suy luận nhân quả thì nhiều khả năng bạn giỏi về thống kê, và từ đó cũng giỏi về học máy.
Nếu tôi đặt điều kiện lên kiến thức về thống kê của bạn, thì lượng kiến thức về học máy của bạn trở nên độc lập với lượng kiến thức về suy luận nhân quả. Như vậy, việc biết về trình độ kiến thức thống kê của bạn cung cấp cho tôi tất cả những thông tin cần thiết để suy ra trình độ kỹ năng học máy của bạn. Tuy nhiên, việc biết về trình độ suy luận nhân quả của bạn sẽ không cung cấp thêm được thông tin gì trong trường hợp này.
Theo nguyên tắc chung, hai biến cùng có một nguyên nhân chung thì phụ thuộc vào nhau, nhưng độc lập với nhau khi chúng ta đặt điều kiện lên nguyên nhân chung. Hoặc,
\[A \not\!\perp\!\!\!\perp B\]and
\[A \!\perp\!\!\!\perp B | C\]Mẫu hình duy nhất chưa được đề cập tới là “đỉnh va chạm”. Đỉnh va chạm xảy ra khi hai mũi tên cùng chỉ vào hay “va chạm” vào một biến. Trong trường hợp này chúng ta có thể nói rằng cả hai biến cùng có một kết quả chung.
g = gr.Digraph()
g.edge("B", "C")
g.edge("A", "C")
g.edge("Y", "X")
g.edge("Z", "X")
g.node("X", "X", color="red")
g.edge("chuyên môn", "thăng tiến")
g.edge("tâng bốc", "thăng tiến")
g
Ví dụ, giả sử có hai cách để thăng tiến trong công việc. Bạn có thể giỏi về chuyên môn hoặc biết cách để tâng bốc cấp trên. Nếu tôi không đặt điều kiện lên sự thăng tiến của bạn, tức là tôi không biết gì về việc bạn có được thăng chức hay không, thì trình độ chuyên môn của bạn và việc bạn giỏi tâng bốc cấp trên là độc lập. Mặt khác, nếu bạn được thăng chức, đột nhiên, việc biết về trình độ chuyên môn của bạn cho tôi biết về “tài năng” nịnh sếp của bạn. Nếu bạn kém trong khoản kiến thức chuyên môn và bạn được thăng chức, thì có nhiều khả năng bạn rất biết cách để nịnh sếp, nếu không thì, bạn biết đấy, bạn đang nằm mơ giữa ban ngày mà thôi. Ngược lại, nếu bạn không giỏi trong khoản tâng bốc người khác, thì bạn phải giỏi về chuyên môn. Hiện tượng này đôi lúc được gọi là sự thanh minh, bởi vì một nguyên nhân đã giải thích kết quả, làm cho nguyên nhân còn lại ít có khả năng xảy ra hơn.
Theo nguyên tắc chung, đặt điều kiện lên một đỉnh va chạm mở ra một đường đi phụ thuộc. Nếu không, sự phụ thuộc không xuất hiện. Hoặc,
\[A \!\perp\!\!\!\perp B\]và
\[A \not\!\perp\!\!\!\perp B | C\]Sau khi biết ba dạng mẫu hình, chúng ta có thể rút ra một quy tắc tổng quát hơn. Một đường đi bị chặn khi và chỉ khi:
- Nó chứa một đỉnh không va chạm đã được đặt điều kiện lên.
- Nó chứa một đỉnh va chạm chưa được đặt điều kiện lên và không có hậu duệ nào bị đặt điều kiện lên.
Đây là một ghi chú ngắn gọn về tính phụ thuộc trong biểu đồ. Tôi tham khảo từ một bài thuyết trình ở Stanford bởi Mark Paskin.
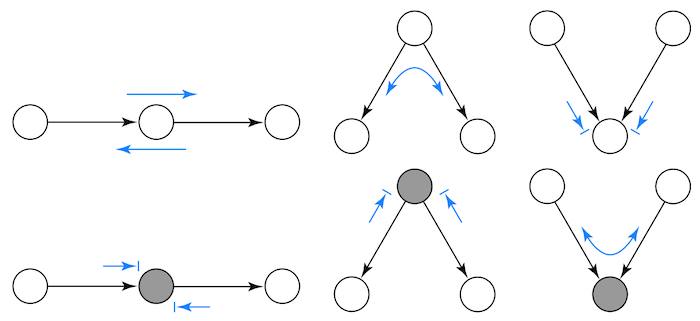
Trong ví dụ cuối cùng này, hãy cố tìm ra một số mối quan hệ độc lập và phụ thuộc trong biểu đồ nhân quả sau đây.
- \(D !\perp!!!\perp C\)?
- \(D !\perp!!!\perp C| A \) ?
- \(D !\perp!!!\perp C| G \) ?
- \(A !\perp!!!\perp F \) ?
- \(A !\perp!!!\perp F|E \) ?
- \(A !\perp!!!\perp F|E,C \) ?
g = gr.Digraph()
g.edge("C", "A")
g.edge("C", "B")
g.edge("D", "A")
g.edge("B", "E")
g.edge("F", "E")
g.edge("A", "G")
g
Answers:
- \(D !\perp!!!\perp C\). Nó chứa một đỉnh va chạm chưa được đặt điều kiện lên.
- \(D \not!\perp!!!\perp C| A \). Nó chứa một đỉnh va chạm đã được đặt điều kiện lên.
- \(D \not!\perp!!!\perp C| G \). Nó chứa hậu duệ của một đỉnh va chạm đã được đặt điều kiện lên. Bạn có thể coi G như một biến đại diện cho A.
- \(A !\perp!!!\perp F \). Nó chứa một đỉnh va chạm, B->E<-F, chưa được đặt điều kiện lên.
- \(A \not!\perp!!!\perp F|E \). Nó chứa một đỉnh va chạm, B->E<-F, đã được đặt điều kiện lên.
- \(A !\perp!!!\perp F|E, C \). Nó chứa một đỉnh va chạm, B->E<-F, đã được đặt điều kiện lên, nhưng nó cũng chứa một đỉnh không va chạm đã được đặt điều kiện lên. Đặt điều kiện trên E mở ra một đường đi, nhưng đặt điều kiện trên C lại đóng đường đi đó.
Hiểu biết về các mô hình biểu đồ nhân quả giúp chúng ta hiểu về các vấn đề xảy ra trong suy luận nhân quả. Như ta đã thấy, chung quy lại các vấn đề luôn dẫn tới thiên lệch.
\[E[Y|T=1] - E[Y|T=0] = \underbrace{E[Y_1 - Y_0|T=1]}_{ATET}\] \[+ \underbrace{\{ E[Y_0|T=1] - E[Y_0|T=0] \}}_{Thiên \ lệch}\]Mô hình biểu đồ cho phép ta tìm ra loại thiên lệch mà ta đang gặp phải và những công cụ cần thiết để giải quyết chúng.
Thiên lệch nhiễu
Một trong những nguyên nhân chủ yếu gây ra thiên lệch là thiên lệch nhiễu. Điều này xảy ra khi sự can thiệp và kết quả cùng có một nguyên nhân chung. Ví dụ, giả sử sự can thiệp là giáo dục và kết quả là thu nhập. Thật khó để xác định tác động nhân quả của giáo dục lên thu nhập bởi cả hai cùng có một nguyên nhân chung: trí tuệ. Vì thế ta có thể lập luận rằng những người có học vấn cao hơn thì kiếm được nhiều tiền hơn đơn giản bởi họ thông minh hơn, chứ không phải bởi họ học nhiều hơn. Để nhận biết tác động nhân quả, chúng ta cần đóng tất cả những đường đi cửa sau giữa sự can thiệp và kết quả. Nếu chúng ta làm như vậy, sẽ chỉ còn duy nhất một tác động còn sót lại là tác động trực tiếp T->Y. Trong ví dụ sau đây, nếu chúng ta cho “trí tuệ” là biến kiểm soát, nghĩa là ta so sánh những người có cùng mức độ thông minh nhưng trình độ học vấn khác nhau, sự khác biệt trong thu nhập sẽ được gây ra duy nhất bởi sự khác biệt về học vấn, bởi mức độ thông minh của mọi người trong thí nghiệm này là như nhau. Vì vậy, để khắc phục thiên lệch nhiễu, chúng ta cần phải kiểm soát tất cả các nguyên nhân chung của sự can thiệp và kết quả.
g = gr.Digraph()
g.edge("X", "T")
g.edge("X", "Y")
g.edge("T", "Y")
g.edge("Trí tuệ", "Học vấn"),
g.edge("Trí tuệ", "Lương"),
g.edge("Học vấn", "Lương")
g
Đáng tiếc rằng không phải lúc nào chúng ta cũng có thể kiểm soát tất cả nguyên nhân chung. Đôi khi có những nguyên nhân chưa biết và những nguyên nhân đã biết mà chúng ta không thể đo lường được. Ví dụ trên về trí tuệ thuộc trường hợp thứ hai. Bất chấp mọi nỗ lực, các nhà khoa học vẫn chưa tìm ra cách đo mức độ thông minh chính xác. Tôi sẽ sử dụng U để ký hiệu các biến không thể đo được ở đây. Bây giờ hãy giả sử rằng trí tuệ không chi phối việc học của bạn một cách trực tiếp. Nó chỉ ảnh hưởng đến việc bạn làm bài như thế nào trong kỳ thi SAT, nhưng chính kết quả bài SAT sẽ ảnh hưởng tới trình độ học vấn của bạn bởi vì nó quyết định khả năng để bạn được nhận vào một trường đại học tốt. Ngay cả khi chúng ta không thể kiểm soát biến không thể đo được trí tuệ, chúng ta có thể kiểm soát được điểm SAT và đóng đường đi cửa sau đó.
g = gr.Digraph()
g.edge("X1", "T")
g.edge("T", "Y")
g.edge("X2", "T")
g.edge("X1", "Y")
g.edge("U", "X2")
g.edge("U", "Y")
g.edge("Thu nhập Gia đình", "Học vấn")
g.edge("Học vấn", "Lương")
g.edge("SAT", "Học vấn")
g.edge("Thu nhập Gia đình", "Lương")
g.edge("Trí tuệ", "SAT")
g.edge("Trí tuệ", "Lương")
g
Trong biểu đồ dưới đây, đặt điều kiện lên X1 và X2, hay là, SAT và thu nhập gia đình, là đủ để đóng tất cả các đường đi cửa sau giữa sự can thiệp và kết quả. Hay nói cách khác, \((Y_0, Y_1) \perp T | X1, X2\). Vì vậy ngay cả khi chúng ta không thể đo lường được tất cả các nguyên nhân chung, chúng ta vẫn có thể thu được sự độc lập có điều kiện nếu chúng ta kiểm soát các biến có thể đo được đóng vai trò trung gian cho tác động của biến không thể đo được trong can thiệp.
Nhưng nếu trường hợp trên không xảy ra thì sao? Điều gì sẽ xảy ra nếu biến không thể đo được trực tiếp gây ra sự can thiệp và kết quả? Trong ví dụ sau, trí tuệ trực tiếp chi phối học vấn và thu nhập. Vì vậy có hiện tượng nhiễu trong quan hệ giữa học vấn (sự can thiệp) và thu nhập (kết quả). Trong trường hợp này, chúng ta không thể kiểm soát biến nhiễu bởi vì nó không thể đo lường được. Những biến này không ở trong đường đi cửa sau, nhưng kiểm soát chúng sẽ giúp giảm (nhưng không triệt tiêu) thiên lệch. Những biến này đôi khi được đề cập đến như những biến đại diện nhiễu.
Trong ví dụ của mình, chúng ta không thể đo lường trí tuệ, nhưng chúng ta có thể đo lường những nguyên nhân của nó, như học vấn của cha và học vấn của mẹ, và một vài tác động như chỉ số IQ hay điểm SAT. Kiểm soát các biến biến đại diện này tuy không đủ để triệt tiêu thiên lệch nhưng vẫn góp phần hạn chế nó.
g = gr.Digraph()
g.edge("X", "U")
g.edge("U", "T")
g.edge("T", "Y")
g.edge("U", "Y")
g.edge("Trí tuệ", "IQ")
g.edge("Trí tuệ", "SAT")
g.edge("Học vấn của cha", "Trí tuệ")
g.edge("Học vấn của mẹ", "Trí tuệ")
g.edge("Trí tuệ", "Học vấn")
g.edge("Học vấn", "Lương")
g.edge("Trí tuệ", "Lương")
g
Thiên lệch chọn
Bây giờ bạn có thể nghĩ rằng bạn nên đưa tất cả những biến có thể đo lường được vào mô hình để chắc chắn rằng mình sẽ không gặp phải thiên lệch nhiễu. Hãy nghĩ kỹ lại nào!

Nguyên nhân chính thứ hai của thiên lệch chính là thiên lệch chọn. Nếu thiên lệch nhiễu xảy ra khi chúng ta không kiểm soát nguyên nhân chung, thiên lệch chọn lại liên quan nhiều hơn tới các kết quả. Một điều đáng để lưu ý là các chuyên gia kinh tế có xu hướng coi tất cả các loại thiên lệch là thiên lệch chọn. Tôi lại cho rằng việc phân biệt giữa thiên lệch chọn và thiên lệch nhiễu rất hữu dụng, vì vậy tôi sẽ bám sát quan điểm này.
Thiên lệch chọn thường xảy ra khi chúng ta kiểm soát nhiều hơn số biến chúng ta cần kiểm soát. Đó có thể là trường hợp khi sự can thiệp và kết quả tiềm năng độc lập biên, nhưng lại trở nên phụ thuộc một khi chúng ta kiểm soát một đỉnh va chạm.
Hãy tưởng tượng bằng một phép màu nào đó cuối cùng bạn cũng có thể ngẫu nhiên hoá biến “học vấn” với mục đích đo lường tác động của nó lên thu nhập. Để chắc chắn rằng bạn không có biến gây nhiễu, bạn kiểm soát một loạt các biến. Trong số đó, bạn kiểm soát biến “đầu tư”. Nhưng sự đầu tư lại không phải là một nguyên nhân chung của học vấn và thu nhập. Thay vào đó, đầu tư lại là kết quả của cả hai. Người có học vấn cao hơn kiếm được nhiều tiền hơn và đầu tư nhiều hơn. Và người kiếm được nhiều tiền hơn cũng đầu tư nhiều hơn. Bởi vì đầu tư là một đỉnh va chạm, bằng cách đặt điều kiện lên biến này, bạn đang mở ra một đường đi thứ hai giữa sự can thiệp và kết quả, và điều này sẽ khiến cho việc đo lường tác động trực tiếp trở nên khó khăn hơn. Nói cách khác, bằng việc kiểm soát biến “đầu tư”, bạn đang nhìn vào nhiều nhóm nhỏ trong tổng thể, mỗi nhóm có mức đầu tư giống nhau, và sau đó bạn tìm tác động của biến “học vấn” lên các nhóm này. Nhưng nếu làm như vậy, bạn đang gián tiếp và vô tình không cho phép thu nhập thay đổi nhiều. Kết quả là bạn sẽ không thể thấy được học vấn tác động lên thu nhập như thế nào bởi vì bạn không cho phép thu nhập thay đổi.
g = gr.Digraph()
g.edge("T", "X")
g.edge("T", "Y")
g.edge("Y", "X")
g.node("X", "X", color="red")
g.edge("Học vấn", "Đầu tư")
g.edge("Học vấn", "Lương")
g.edge("Lương", "Đầu tư")
g
Để chứng minh tại sao lại như vậy trong trường hợp nếu như đầu tư và giáo dục chỉ nhận hai giá trị. Mọi người sẽ đầu tư hoặc không. Họ sẽ được học hành hoặc không. Ban đầu, chúng ta không kiểm soát sự đầu tư, thiên lệch bằng không \(E[Y_0|T=1] - E[Y_0|T=0] = 0\) bởi giáo dục được ngẫu nhiên hoá. Điều này có nghĩa rằng thu nhập mọi người nhận được trong trường hợp họ không được học hành \(Lương_0\) là giống nhau bất kể họ nhận được sự can thiệp giáo dục hay không. Nhưng điều gì sẽ xảy ra nếu chúng ta đặt điều kiện lên sự đầu tư?
Nhìn vào những người đầu tư, chúng ta có thể thấy trường hợp \(E[Y_0|T=0, ĐT=1] > E[Y_0|T=1, ĐT=1]\). Nói cách khác, những người có khả năng kiếm được tiền từ đầu tư không qua học hành thì họ cũng chẳng cần học hành để có lương cao. Chính vì lý do này, thu nhập của một người, \(Lương_0|T=0\), có khả năng cao hơn thu nhập của người được học hành sẽ nhận được trong trường hợp họ không được học hành, \(Lương_0|T=1\). Chúng ta có thể áp dụng cách lý luận tương tự cho những trường hợp không đầu tư, trong đó \(E[Y_0|T=0, ĐT=0] > E[Y_0|T=1, ĐT=0]\). Những người không đầu tư và được học hành, có khả năng sẽ có mức thu nhập thấp hơn, nếu họ không được học hành, nếu so với những người không đầu tư và cũng không được học hành.
Để sử dụng một lập luận biểu đồ thuần tuý, nếu một người nào đó đầu tư, việc biết rằng họ có trình độ học vấn giải thích cho nguyên nhân thứ hai là thu nhập. Đặt điều kiện lên đầu tư, học vấn cao hơn đi kèm với mức thu nhập thấp và chúng ta có thiên lệch âm \(E[Y_0|T=0, ĐT=i] > E[Y_0|T=1, ĐT=i]\).
Một lưu ý nhỏ, tất cả những điều chúng ta vừa thảo luận đều đúng nếu chúng ta đặt điều kiện trên bất cứ hậu duệ nào của một kết quả chung.
g = gr.Digraph()
g.edge("T", "X")
g.edge("T", "Y")
g.edge("Y", "X")
g.edge("X", "S")
g.node("S", "S", color="red")
g
Điều tương tự xảy ra khi chúng ta đặt điều kiện trên một biến trung gian của can thiệp. Một biến trung gian là một biến nằm giữa sự can thiệp và kết quả. Nó đóng vai trò trung gian cho tác động nhân quả. Ví dụ, tiếp tục giả sử rằng bạn có thể ngẫu nhiên hoá giáo dục. Nhưng để cho chắc chắn, bạn quyết định kiểm soát xem liệu người đó có phải là nhân viên văn phòng hay không. Một lần nữa, điều kiện này làm thiên lệch sự ước lượng tác động nhân quả. Lần này, không phải bởi vì nó mở ra một đường đi cửa trước với một đỉnh va chạm, mà bởi vì nó đóng một trong những con đường mà sự can thiệp vận hành thông qua nó. Trong ví dụ của chúng ta, có được công việc văn phòng là một cách để những người có học vấn cao đạt được thu nhập cao hơn. Bằng việc kiểm soát nó, chúng ta đã đóng đi con đường này và chỉ giữ lại kênh tác động trực tiếp của giáo dục lên thu nhập.
g = gr.Digraph()
g.edge("T", "X")
g.edge("T", "Y")
g.edge("X", "Y")
g.node("X", "X", color="red")
g.edge("học vấn", "văn phòng")
g.edge("học vấn", "lương")
g.edge("văn phòng", "lương")
g
Để đưa ra một lập luận cho kết quả tiềm năng, chúng ta biết rằng bởi sự ngẫu nhiên hoá, thiên lệch bằng không \(E[Y_0|T=0] - E[Y_0|T=1] = 0\). Tuy nhiên, nếu chúng ta đặt điều kiện lên những nhân viên văn phòng, chúng ta có \(E[Y_0|T=0, VP=1] > E[Y_0|T=1, VP=1]\). Điều này bởi vì những người cố gắng để đạt được công việc văn phòng mặc dù không được học hành có khả năng làm việc chăm chỉ hơn những người được học hành để có được công việc tương tự. Với lập luận tương tự, \(E[Y_0|T=0, VP=0] > E[Y_0|T=1, VP=0]\), vì những người không có được công việc văn phòng mặc dù được giáo dục có khả năng làm việc kém chăm chỉ hơn những người cũng không có được công việc đó và không được học hành.
Trong trường hợp của chúng ta, việc đặt điều kiện lên biến trung gian gây ra thiên lệch âm. Nó làm cho tác động của học vấn có vẻ thấp hơn thực tế. Trong trường hợp này, nguyên nhân là do tác động nhân quả tích cực. Trong trường hợp tiêu cực, việc đặt điều kiện lên biến trung gian sẽ gây ra thiên lệch dương. Trong tất cả các trường hợp, cách đặt điều kiện này đều khiến cho tác động yếu hơn so với thực tế.
Nói một cách dễ hiểu hơn, giả sử rằng bạn phải chọn giữa hai ứng viên cho một vị trí trong công ty. Cả hai đều có những thành tựu về mặt chuyên môn ấn tượng như nhau, nhưng một người không có bằng đại học. Bạn sẽ chọn ứng viên nào? Rõ ràng, bạn nên chọn ứng viên không có bằng đại học, bởi người này đã cố gắng để đạt được những thành tựu tương tự như ứng viên kia dù trong điều kiện khó khăn và kém thuận lợi hơn.

Tài liệu tham khảo
Tôi muốn dành loạt bài viết này để vinh danh Joshua Angrist, Alberto Abadie and Christopher Walters vì khóa học Kinh tế lượng tuyệt cú mèo của họ. Phần lớn ý tưởng trong loạt bài này được lấy từ các bài giảng của họ được tổ chức bởi Hiệp hội Kinh tế Mĩ. Theo dõi các bài giảng này là những gì tôi làm trong suốt năm 2020 khó nhằn.
Tôi cũng muốn giới thiệu cuốn sách lý thú của Angrist. Chúng cho tôi thấy Kinh tế lượng, hoặc ‘Lượng theo cách họ gọi không chỉ vô cùng hữu ích mà còn rất vui.
Tài liệu tham khảo cuối cùng của tôi là cuốn sách của Miguel Hernan and Jamie Robins. Nó là người bạn đồng hành tin cậy với tôi khi trả lời những câu hỏi nhân quả khó nhằn.
Bảng Thuật ngữ
| Thuật ngữ | Tiếng Anh |
|---|---|
| biến | variable |
| biến không thể đo được | unmeasured variable |
| biến ngẫu nhiên | random variable |
| biến nhiễu | confounder, confounding variable |
| biến trung gian | mediator, intermediary variable |
| biến đại diện | proxy, surrogate variable |
| biến đại diện nhiễu | surrogate confounder |
| biểu đồ | graph |
| cạnh | edge |
| giả thiết | assumption |
| học máy | machine learning |
| kết quả | outcome |
| kết quả tiềm năng | potential outcome |
| mô hình biểu đồ | graphical model |
| mô hình biểu đồ nhân quả | causal graphical model |
| nhiễu | confounding |
| quan hệ nhân quả | causality, causation, causal relationship |
| suy luận nhân quả | causal inference, causal reasoning |
| thiên lệch | bias |
| thiên lệch chọn | selection bias |
| thiên lệch nhiễu | confounding bias, confouding bias |
| thống kê | statistics |
| tổng thể | population |
| đỉnh | node |
| đỉnh không va chạm | non collider |
| đỉnh va chạm | collider |
| độc lập biên | marginal independent |
| độc lập có điều kiện | conditionally independent, conditional independence |











Comments