Phương pháp Ghép cặp

SUY LUẬN NHÂN QUẢ VỚI PYTHON - KỲ 10

Bài viết này thuộc chuỗi bài viết về “Suy luận Nhân quả với Python”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây

Để hiểu một cách trực quan về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “60 Giây Nhân quả” tại đây

Rốt cuộc Hồi quy đã làm gì?

Tới thời điểm hiện tại, hồi quy đã làm rất tốt việc kiểm soát các biến thêm vào khi chúng ta thực hiện so sánh giữa nhóm được can thiệp và nhóm đối chứng. Nếu ta có tính chất độc lập, \((Y_0, Y_1)\perp T | X\), thì hồi quy có thể xác định ATE bằng cách kiểm soát X. Cách thức mà hồi quy thực hiện như thể một phép màu vậy. Để dễ hiểu hơn, hãy nhớ lại trường hợp khi tất cả các biến X đều là biến giả. Trong trường hợp này, hồi quy chia dữ liệu thành các ô chứa biến giả và tính hiệu của các giá trị trung bình của nhóm được can thiệp và nhóm đối chứng. Hiệu của các giá trị trung bình giữ cho X không đổi, bởi vì chúng ta đang thực hiện trên một ô cố định của biến giả X. Phương pháp này như thể chúng ta đang tính toán \(E[Y|T=1] - E[Y|T=0] | X=x\), trong đó \(x\) là ô chứa biến giả (ví dụ, tất cả các biến giả được cho bằng 1). Sau đó, hồi quy kết hợp ước lượng trong mỗi ô để thu được giá trị ATE cuối cùng bằng cách đặt trọng số lên mỗi ô tỷ lệ với phương sai của can thiệp lên nhóm đó.

import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np
from matplotlib import style
from matplotlib import pyplot as plt
import statsmodels.formula.api as smf

import graphviz as gr

%matplotlib inline

style.use("fivethirtyeight")

Ví dụ, giả sử chúng ta muốn ước lượng tác dụng của một loại thuốc, ta có 6 bệnh nhân nam và 4 bệnh nhân nữ. Biến phụ thuộc là số ngày nằm viện và chúng ta hy vọng rằng loại thuốc này có thể làm giảm số ngày nằm viện. Đối với bệnh nhân nam, tác động nhân quả thực bằng -3, vì thế loại thuốc này làm giảm bớt số ngày nằm viện khoảng 3 ngày. Đối với bệnh nhân nữ, hệ số này bằng -2. Để làm cho ví dụ trở nên thú vị hơn, giả sử nam giới bị ảnh hưởng bởi căn bệnh này nhiều hơn và có thời gian nằm viện lâu hơn. Họ cũng sử dụng nhiều thuốc hơn. Chỉ 1 trong số 6 bệnh nhân nam không sử dụng thuốc. Mặt khác, nữ giới có sức đề kháng cao hơn đối với căn bệnh này, vì thế thời gian nằm viện của họ ngắn hơn. 50% bệnh nhân nữ sử dụng thuốc.

drug_example = pd.DataFrame(dict(
    sex= ["M","M","M","M","M","M", "W","W","W","W"],
    drug=[1,1,1,1,1,0,   1,0,1,0],
    days=[5,5,5,5,5,8,  2,4,2,4]
))

Lưu ý rằng sự so sánh đơn giản giữa nhóm được can thiệp và nhóm đối chứng tạo ra tác động thiên lệch âm, nghĩa là, thuốc có vẻ kém hiệu quả hơn thực tế. Điều này đã được dự báo trước, bởi chúng ta đã bỏ qua biến nhiễu giới tính. Trong trường hợp này, ATE được ước lượng nhỏ hơn thực tế bởi nam sử dụng nhiều thuốc hơn và bị ảnh hưởng bởi căn bệnh này nhiều hơn.

drug_example.query("drug==1")["days"].mean() - drug_example.query("drug==0")["days"].mean()

-1.1904761904761898

Vì tác động thực cho nam bằng -3 và cho nữ bằng -2, ta có ATE \(ATE=\dfrac{(-3*6) + (-2*4)}{10}=-2.6\)

Ước lượng này được thực hiện bởi 1) chia dữ liệu thành các ô chứa biến nhiễu, trong trường hợp này, nam và nữ, 2) ước lượng tác động lên từng ô, và 3) kết hợp ước lượng với bình quân gia quyền, trong đó trọng số là kích thước mẫu của ô hay nhóm biến giải thích. Nếu chúng ta có cùng kích thước mẫu của nam và nữ trong dữ liệu, ước lượng ATE sẽ nằm ngay giữa ATE của 2 nhóm, -2.5. Vì chúng ta có nhiều nam hơn nữ trong dữ liệu, ước lượng ATE sẽ gần với ATE của nam hơn. Đây được gọi là ước lượng phi tham số, vì nó không đặt giả thiết lên quy luật tạo lập dữ liệu.

Nếu chúng ta kiểm soát giới tính bằng cách sử dụng hồi quy, chúng ta sẽ thêm giả thiết về tuyến tính. Hồi quy sẽ chia dữ liệu thành nam và nữ, và ước lượng tác động của cả hai nhóm. Đến giờ mọi thứ có vẻ trơn tru. Tuy nhiên, sự kết hợp tác động của từng nhóm không đặt trọng số của chúng theo kích thước mẫu. Thay vào đó, hồi quy sử dụng trọng số tỷ lệ với phương sai của can thiệp lên nhóm đó. Trong trường hợp của chúng ta, phương sai của can thiệp lên nam nhỏ hơn nữ, bởi vì chỉ có duy nhất một nam trong nhóm đối chứng. Một cách chính xác, phương sai của T cho nam là \(0.139=1/6(1 - 1/6)\) và cho nữ là \(0.25=2/4(1 - 2/4)\). Vì vậy, hồi quy sẽ đặt trọng số cao hơn cho nữ trong ví dụ của chúng ta, và ATE sẽ gần với ATE của nữ (bằng -2) hơn.

smf.ols('days ~ drug + C(sex)', data=drug_example).fit().summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	7.5455	0.188	40.093	0.000	7.100	7.990
C(sex)[T.W]	-3.3182	0.176	-18.849	0.000	-3.734	-2.902
drug	-2.4545	0.188	-13.042	0.000	-2.900	-2.010

Kết quả này hợp lý hơn với các biến giả, tuy nhiên, theo một cách kỳ lạ, hồi quy vẫn giữ các biến liên tục không đổi trong khi ước lượng tác động. Hơn nữa, với các biến liên tục, ATE sẽ ngả theo các biến giải thích có phương sai lớn hơn.

Vậy là chúng ta đã thấy những đặc trưng của hồi quy. Nó tuyến tính, có tham số, ngả theo các thuộc tính có phương sai lớn… Điều này có thể tốt hoặc xấu tuỳ thuộc vào bối cảnh. Vì thế, nhận biết được các phương pháp khác để kiểm soát biến nhiễu rất quan trọng. Chúng không chỉ đơn thuần là các công cụ bổ sung vào nhóm các phương pháp nhân quả của bạn, mà còn mở rộng sự hiểu biết của chúng ta về nhiều phương pháp khác để giải quyết nhiễu. Do vậy, tiếp theo tôi sẽ giới thiệu về Mô Hình Ước Lượng Phân Lớp!

Mô Hình Ước Lượng Phân Lớp

Nếu muốn ước lượng một số tác động nhân quả, như tác động của đào tạo nghiệp vụ lên thu nhập, và can thiệp không được chỉ định ngẫu nhiên, chúng ta cần phải đề phòng các biến nhiễu. Có thể do chỉ những người có quyết tâm cao độ mới theo học các khoá đào tạo, và họ có thu nhập cao hơn bất kể họ có được đào tạo nghiệp vụ hay không. Chúng ta cần phải ước lượng tác động của chương trình đào tạo lên nhiều nhóm nhỏ gồm các cá nhân có quyết tâm hoặc bất kỳ biến nhiễu nào khác ngang ngửa nhau.

Một cách tổng quát hơn, trong trường hợp khó ước lượng một số tác động nhân quả mà chúng ta quan tâm do nhiễu của một vài biến X, điều chúng ta cần phải làm là so sánh can thiệp và kiểm soát trong những nhóm nhỏ có X giống nhau. Nếu chúng ta có tính chất độc lập có điều kiện, \((Y_0, Y_1)\perp T | X\), thì ATE có thể được biểu diễn như sau.

\[ATE = \int(E[Y|X, T=1] - E[Y|X, T=0])dP(x)\]

Nhiệm vụ của tích phân này là tính ATE bằng cách cộng tất cả hiệu của các giá trị trung bình cho mỗi khoảng vô cùng nhỏ dọc theo phân phối giá trị của các thuộc tính X. Một cách khác để hiểu điều này là liên tưởng tới một tập hợp các biến X rời rạc. Trong trường hợp này, ta có thể nói rằng các biến X đảm nhận K ô khác nhau \({X_1, X_2, …, X_k}\) và điều chúng ta đang làm là tính toán tác động can thiệp trong từng ô và kết hợp chúng lại thành ATE. Trong trường hợp biến rời rạc như này, chuyển từ tích phân thành tổng, chúng ta có thể suy ra mô hình ước lượng phân lớp.

\[\hat{ATE} = \sum^K_{i=0}(\bar{Y}_{k1} - \bar{Y}_{k0}) * \dfrac{N_k}{N}\]

trong đó \(\bar{Y_{k1}}\) là kết quả trung bình của nhóm được can thiệp trong ô k, \(\bar{Y_{k0}}\) là kết quả trung bình của nhóm đối chứng trong ô k, và \(N_{k}\) là số các quan sát trong ô k. Như vậy, chúng ta đang tính toán LATE cho từng ô và kết hợp chúng bằng cách sử dụng bình quân gia quyền, trong đó trọng số là kích thước mẫu của từng ô. Trong ví dụ về thuốc của chúng ta ở trên, nó là ước lượng đầu tiên cho chúng ta kết quả -2.6.

Mô Hình Ước Lượng Ghép Cặp

Trong thực tế, mô hình ước lượng phân lớp không được sử dụng nhiều (chúng ta sẽ sớm biết tại sao do lời nguyền đa chiều) nhưng nó cho chúng ta một cách nhìn bằng trực giác về điều mà một mô hình ước lượng suy luận nhân quả nên làm, và cách nó kiểm soát các biến nhiễu. Điều này cho phép chúng ta khám phá các loại mô hình ước lượng khác, ví dụ như Mô Hình Ước Lượng Ghép Cặp.

Ý tưởng khá tương tự. Vì một số loại biến nhiễu X khiến ban đầu nhóm được can thiệp và nhóm đối chứng không tương đồng, chúng ta có thể làm chúng tương đồng bằng cách ghép mỗi đối tượng được can thiệp với một đối chứng tương tự. Quá trình này giống như chúng ta đang đi tìm một “người anh em song sinh” đối chứng cho mỗi một đối tượng được can thiệp. Bằng cách so sánh như vậy, nhóm can thiệp và nhóm đối chứng trở nên tương đồng.

Ví dụ, giả sử rằng ta đang muốn ước lượng tác động của một chương trình đào tạo lên thu nhập. Dưới đây là thông tin các học viên.

trainee = pd.read_csv("./data/trainees.csv")
trainee.query("trainees==1")

	unit	trainees	age	earnings
0	1	1	28	17700
1	2	1	34	10200
2	3	1	29	14400
3	4	1	25	20800
4	5	1	29	6100
5	6	1	23	28600
6	7	1	33	21900
7	8	1	27	28800
8	9	1	31	20300
9	10	1	26	28100
10	11	1	25	9400
11	12	1	27	14300
12	13	1	29	12500
13	14	1	24	19700
14	15	1	25	10100
15	16	1	43	10700
16	17	1	28	11500
17	18	1	27	10700
18	19	1	28	16300

Và thông tin của những người không phải là học viên:

trainee.query("trainees==0")

	unit	trainees	age	earnings
19	20	0	43	20900
20	21	0	50	31000
21	22	0	30	21000
22	23	0	27	9300
23	24	0	54	41100
24	25	0	48	29800
25	26	0	39	42000
26	27	0	28	8800
27	28	0	24	25500
28	29	0	33	15500
29	31	0	26	400
30	32	0	31	26600
31	33	0	26	16500
32	34	0	34	24200
33	35	0	25	23300
34	36	0	24	9700
35	37	0	29	6200
36	38	0	35	30200
37	39	0	32	17800
38	40	0	23	9500
39	41	0	32	25900

Nếu ta làm một phép so sánh đơn giản giữa các giá trị trung bình, chúng ta thấy rằng học viên kiếm được ít tiền hơn những người không tham chương trình đào tạo.

trainee.query("trainees==1")["earnings"].mean() - trainee.query("trainees==0")["earnings"].mean()

-4297.49373433584

Tuy nhiên, nếu nhìn vào bảng trên, ta thấy học viên thường trẻ hơn những người không tham gia, điều này ám chỉ tuổi tác có thể là một biến nhiễu. Hãy sử dụng phương pháp ghép cặp lên tuổi tác để điều chỉnh điều này. Chúng ta sẽ lấy đối tượng 1 từ nhóm can thiệp và ghép cặp nó với đối tượng 27, vì cả hai cùng 28 tuổi. Đối tượng 2 sẽ được ghép cặp với đối tượng 34, đối tượng 3 với đối tượng 37, đối tượng 4 với đối tượng 35… Đối với đối tượng 5, chúng ta cần phải tìm một người nào đó 29 tuổi từ nhóm đối chứng, và đó là đối tượng 37, tuy nhiên đối tượng 37 đã được ghép cặp trước đó. Không thành vấn đề, chúng ta có thể sử dụng cùng một đối tượng nhiều lần. Nếu có nhiều hơn một đối tượng có thể ghép cặp với một đối tượng khác, ta chọn ngẫu nhiên một trong số chúng.

Đây là bộ dữ liệu đã được ghép cặp cho 7 đối tượng đầu

# make dataset where no one has the same age
unique_on_age = (trainee
                 .query("trainees==0")
                 .drop_duplicates("age"))

matches = (trainee
           .query("trainees==1")
           .merge(unique_on_age, on="age", how="left", suffixes=("_t_1", "_t_0"))
           .assign(t1_minuts_t0 = lambda d: d["earnings_t_1"] - d["earnings_t_0"]))

matches.head(7)

	unit_t_1	trainees_t_1	age	earnings_t_1	unit_t_0	trainees_t_0	earnings_t_0	t1_minuts_t0
0	1	1	28	17700	27	0	8800	8900
1	2	1	34	10200	34	0	24200	-14000
2	3	1	29	14400	37	0	6200	8200
3	4	1	25	20800	35	0	23300	-2500
4	5	1	29	6100	37	0	6200	-100
5	6	1	23	28600	40	0	9500	19100
6	7	1	33	21900	29	0	15500	6400

Chú ý cách cột cuối cùng thể hiện sự khác biệt về thu nhập giữa nhóm can thiệp và nhóm đối chứng trong một cặp. Nếu chúng ta lấy giá trị trung bình của cột cuối cùng thì ta thu được ước lượng ATET khi kiểm soát tuổi tác. Lưu ý rằng ước lượng bây giờ mang giá trị dương trong khi trước đó nó mang giá trị âm khi ta tính toán hiệu của các giá trị trung bình.

matches["t1_minuts_t0"].mean()

2457.8947368421054

Tuy nhiên đây là một ví dụ giả định, được đưa ra chỉ nhằm mục đích giới thiệu phương pháp ghép cặp. Trong thực tế, chúng ta thường sử dụng nhiều hơn một thuộc tính và các đối tượng không hoàn toàn khớp với nhau. Trong trường hợp này, chúng ta phải xác định một vài phép đo khoảng cách để so sánh khoảng cách giữa các đối tượng. Một thước đo phổ biến là khoảng cách Euclid \(||X_i - X_j||\). Tuy nhiên, hiệu số này không cố định theo độ lớn của các thuộc tính. Có có nghĩa các thuộc tính như tuổi tác, cỡ vài chục, sẽ ít ảnh hưởng hơn trong phép tính khoảng cách Euclid so với các thuộc tính khác như thu nhập vào cỡ vài trăm. Vì lý do này, trước khi áp dụng khoảng cách Euclid, chúng ta cần quy đổi các thuộc tính sao cho chúng có độ lớn tương tự nhau.

Sau khi xác định thước đo khoảng cách, chúng ta có thể xác định các cặp dựa trên láng giềng gần nhất với mẫu mà chúng ta muốn ghép cặp. Chúng ta có thể biểu diễn mô hình ước lượng ghép cặp bằng công thức toán học như sau

\[\hat{ATE} = \frac{1}{N} \sum^N_{i=0} (2T_i - 1)\big(Y_i - Y_{jm}(i)\big)\]

trong đó \(Y_{jm}(i)\) là mẫu từ nhóm được can thiệp khác gần nhất với \(Y_i\). Chúng ta sử dụng \(2T_i - 1\) để ghép cặp theo cả hai cách: nhóm được can thiệp với nhóm đối chứng, và nhóm đối chứng với nhóm được can thiệp.

Để kiểm tra mô hình ước lượng này, hãy xem xét một ví dụ về thuốc. Một lần nữa, chúng ta muốn tìm hiểu tác dụng của thuốc lên số ngày hồi phục. Đáng tiếc, tác dụng của thuốc bị gây nhiễu bởi mức độ nghiêm trọng của bệnh, giới tính, và tuổi tác. Chúng ta có lý do để tin rằng bệnh nhân với tình trạng nặng hơn có nhiều khả năng sử dụng thuốc hơn.

med = pd.read_csv("./data/medicine_impact_recovery.csv")
med.head()

	sex	age	severity	medication	recovery
0	0	35.049134	0.887658	1	31
1	1	41.580323	0.899784	1	49
2	1	28.127491	0.486349	0	38
3	1	36.375033	0.323091	0	35
4	0	25.091717	0.209006	0	15

Nếu chúng ta nhìn vào hiệu của các giá trị trung bình, \(E[Y|T=1]-E[Y|T=0]\), tính trung bình nhóm được can thiệp cần nhiều hơn 16,9 ngày để hồi phục so với nhóm đối chứng. Điều này có thể gây ra bởi nhiễu, vì chúng ta không mong đợi khả năng thuốc gây hại cho người bệnh.

med.query("medication==1")["recovery"].mean() - med.query("medication==0")["recovery"].mean()

16.895799546498726

Để điều chỉnh thiên lệch, chúng ta sẽ kiểm soát X qua phương pháp ghép cặp. Đầu tiên, chúng ta cần quy đổi các thuộc tính, nếu không thì, các thuộc tính như tuổi tác sẽ có nhiều ảnh hưởng hơn các thuộc tính khác như mức độ nghiêm trọng của bệnh khi chúng ta tính toán khoảng cách giữa các điểm. Để làm điều này, chúng ta có thể chuẩn hoá các thuộc tính.

# scale features
X = ["severity", "age", "sex"]
y = "recovery"

med = med.assign(**{f: (med[f] - med[f].mean())/med[f].std() for f in X})
med.head()

	sex	age	severity	medication	recovery
0	-0.996980	0.280787	1.459800	1	31
1	1.002979	0.865375	1.502164	1	49
2	1.002979	-0.338749	0.057796	0	38
3	1.002979	0.399465	-0.512557	0	35
4	-0.996980	-0.610473	-0.911125	0	15

Giờ tới phần ghép cặp. Thay vì tự code phương trình ghép cặp, chúng ta có thể sử dụng thuật toán K láng giềng gần nhất từ Sklearn. Thuật toán này dự đoán bằng cách tìm các điểm dữ liệu gần nhất trong ước lượng hoặc tập huấn luyện.

Đối với phương pháp ghép cặp, chúng ta cần 2 mô hình. Thứ nhất là mt0, sẽ lưu trữ các điểm đối chứng và tìm các cặp trong nhóm đối chứng khi được yêu cầu. Thứ hai là mt1 sẽ lưu trữ các điểm được can thiệp và tìm các cặp trong nhóm can thiệp khi được yêu cầu. Sau bước này, chúng ta có thể sử dụng các mô hình KNN này để dự đoán các cặp của chúng ta.

from sklearn.neighbors import KNeighborsRegressor

treated = med.query("medication==1")
untreated = med.query("medication==0")

mt0 = KNeighborsRegressor(n_neighbors=1).fit(untreated[X], untreated[y])
mt1 = KNeighborsRegressor(n_neighbors=1).fit(treated[X], treated[y])

predicted = pd.concat([
    # find matches for the treated looking at the untreated knn model
    treated.assign(match=mt0.predict(treated[X])),
    
    # find matches for the untreated looking at the treated knn model
    untreated.assign(match=mt1.predict(untreated[X]))
])

predicted.head()

	sex	age	severity	medication	recovery	match
0	-0.996980	0.280787	1.459800	1	31	39.0
1	1.002979	0.865375	1.502164	1	49	52.0
7	-0.996980	1.495134	1.268540	1	38	46.0
10	1.002979	-0.106534	0.545911	1	34	45.0
16	-0.996980	0.043034	1.428732	1	30	39.0

Với các cặp, chúng ta có thể áp dụng công thức của mô hình ước lượng ghép cặp

\[\hat{ATE} = \frac{1}{N} \sum^N_{i=0} (2T_i - 1)\big(Y_i - Y_{jm}(i)\big)\]

np.mean((2*predicted["medication"] - 1)*(predicted["recovery"] - predicted["match"]))

-0.9954

Sử dụng phương pháp ghép cặp này, chúng ta thấy tác dụng của thuốc không còn mang giá trị dương. Điều này có nghĩa là, khi kiểm soát X, tính trung bình thuốc giảm số ngày hồi phục xuống khoảng 1 ngày. Đây là một bước tiến lớn so với ước lượng thiên lệch trước đo dự đoán tăng 16,9 ngày.

Tuy nhiên, chúng ta vẫn có thể làm tốt hơn nữa.

Thiên Lệch Ghép Cặp

Vậy hoá ra mô hình ước lượng ghép cặp chúng ta vừa thiết kế bị thiên lệch. Để hiểu điều này, hãy cùng xem xét mô hình ước lượng ATET, thay vì ATE, vì biểu diễn nó đơn giản hơn. Nguyên lý tương tự cũng áp dụng cho ATE.

\[\hat{ATET} = \frac{1}{N_1}\sum (Y_i - Y_j(i))\]

trong đó \(N_1\) là số lượng đối tượng được can thiệp và \(Y_j(i)\) là các đối chứng và được ghép cặp với đối tượng được can thiệp i. Để kiểm tra thiên lệch, chúng ta hy vọng có thể áp dụng Định Luật Giới Hạn Trung Tâm để cho đại lượng dưới đây hội tụ về phân phối chuẩn với giá trị trung bình bằng 0.

\[\sqrt{N_1}(\hat{ATET} - ATET)\]

Tuy nhiên, điều này không phải lúc nào cũng xảy ra. Nếu chúng ta xác định kết quả trung bình của nhóm đối chứng với X cho sẵn, \(\mu_0(x)=E[Y|X=x, T=0]\), hội tụ về 0 sẽ xảy ra (tuy nhiên tôi đã bỏ qua cách chứng minh điều này bởi vì nó hơi xa vấn đề cần tập trung của chúng ta ở đây).

\[E[\sqrt{N_1}(\hat{ATET} - ATET)] = E[\sqrt{N_1}(\mu_0(X_i) - \mu_0(X_j(i)))]\]

\(\mu_0(X_i) - \mu_0(X_j(i))\) không dễ hiểu chút nào, vì vậy hãy xem xét nó một cách cẩn trọng. \(\mu_0(X_i)\) là kết quả Y của đối tượng i được can thiệp nếu đối tượng i đối chứng. Như vậy, nó là kết quả giả tưởng của đối tượng i. \(\mu_0(X_j(i))\) là kết quả của đối tượng j đối chứng và được ghép cặp với đối tượng i. Nó cũng là \(Y_0\), nhưng của đối tượng j. Chỉ trong trường hợp này, nó mới là kết quả thực, vì j thuộc nhóm đối chứng. Bởi j và i chỉ tương tự nhau, chứ không giống nhau, nên biểu thức trên khó có khả năng nhận giá trị bằng 0. Hay nói cách khác, vì \(X_i \approx X_j \) nên \(Y_{0i} \approx Y_{0j} \).

Khi chúng ta tăng kích thước mẫu, sẽ có nhiều đối tượng hơn để ghép cặp, vì thế chênh lệch giữa đối tượng i và đối tượng j cũng sẽ nhỏ hơn. Tuy nhiên, sự chênh lệch này hội tụ chậm dần về 0. Hệ quả là \(E[\sqrt{N_1}(\mu_0(X_i) - \mu_0(X_j(i)))]\) có thể không hội tụ về 0, bởi phần tăng của \(\sqrt{N_1}\) nhanh hơn phần giảm của \((\mu_0(X_i) - \mu_0(X_j(i)))\).

Thiên lệch phát sinh khi sự khác biệt trong việc ghép cặp lớn. May mắn thay, chúng ta biết cách để điều chỉnh nó. Mỗi một quan sát tạo ra \((\mu_0(X_i) - \mu_0(X_j(i)))\) thiên lệch vì thế tất cả điều chúng ta cần làm là trừ đi phần này trong từng cặp được ghép trong mô hình ước lượng. Để làm được điều này, chúng ta có thể thay thế \(\mu_0(X_j(i))\) bằng một loại ước lượng của đại lượng \(\hat{\mu_0}(X_j(i))\), có thể thu được bằng một số mô hình như hồi quy tuyến tính. Do đó, mô hình ước lượng ATE được biểu diễn lại bằng phương trình sau

\[\hat{ATET} = \frac{1}{N_1}\sum \big((Y_i - Y_{j(i)}) - (\hat{\mu_0}(X_i) - \hat{\mu_0}(X_{j(i)}))\big)\]

trong đó \(\hat{\mu_0}(x)\) là một số ước lượng của \(E[Y|X, T=0]\), ví dụ như hồi quy tuyến tính chỉ hồi quy trên mẫu đối chứng.

from sklearn.linear_model import LinearRegression

# fit the linear regression model to estimate mu_0(x)
ols0 = LinearRegression().fit(untreated[X], untreated[y])
ols1 = LinearRegression().fit(treated[X], treated[y])

# find the units that match to the treated
treated_match_index = mt0.kneighbors(treated[X], n_neighbors=1)[1].ravel()

# find the units that match to the untreatd
untreated_match_index = mt1.kneighbors(untreated[X], n_neighbors=1)[1].ravel()

predicted = pd.concat([
    (treated
     # find the Y match on the other group
     .assign(match=mt0.predict(treated[X])) 
     
     # build the bias correction term
     .assign(bias_correct=ols0.predict(treated[X]) - ols0.predict(untreated.iloc[treated_match_index][X]))),
    (untreated
     .assign(match=mt1.predict(untreated[X]))
     .assign(bias_correct=ols1.predict(untreated[X]) - ols1.predict(treated.iloc[untreated_match_index][X])))
])

predicted.head()

	sex	age	severity	medication	recovery	match	bias_correct
0	-0.996980	0.280787	1.459800	1	31	39.0	4.404034
1	1.002979	0.865375	1.502164	1	49	52.0	12.915348
7	-0.996980	1.495134	1.268540	1	38	46.0	1.871428
10	1.002979	-0.106534	0.545911	1	34	45.0	-0.496970
16	-0.996980	0.043034	1.428732	1	30	39.0	2.610159

Một câu hỏi ngay lập tức xuất hiện là: không phải điều này phủ định sự cần thiết của ghép cặp hay sao? Nếu chúng ta chaỵ một hồi quy tuyến tính, tại sao chúng ta không chỉ sử dụng nó, thay vì một mô hình phức tạp. Đây là một luận điểm có lý, vì vậy tôi sẽ dành thời gian để giải đáp nó.

Thứ nhất, hồi quy tuyến tính mà chúng ta đang ước lượng không giúp ngoại suy theo trục can thiệp để thu được tác động can thiệp. Thay vào đó, mục đích của nó đơn giản chỉ là để điều chỉnh thiên lệch. Hồi quy tuyến tính ở đây có tính chất cục bộ, theo nghĩa nó không tìm cách xác định nhóm can thiệp sẽ ra sao nếu nó trông giống như nhóm đối chứng. Nó không thực hiện việc ngoại suy. Điều này được xử lý bởi phương pháp ghép cặp. Phần cốt lõi của mô hình ước lượng này vẫn là phương pháp ghép cặp. Tóm lại điều tôi muốn chỉ ra ở đây là OLS là phần thứ yếu của mô hình ước lượng này.

Thứ hai, phương pháp ghép cặp là mô hình ước lượng phi tham số. Nó không đưa ra giả định tuyến tính hay bất cứ giả định nào của mô hình có tham số. Như vậy, nó linh hoạt hơn hồi quy tuyến tính và có thể áp dụng trong những tình huống mà hồi quy tuyến tính không phù hợp, cụ thể là những trường hợp phi tuyến tính rất mạnh.

Điều này liệu có nghĩa rằng bạn nên chỉ sử dụng phương pháp ghép cặp? Hmm, đây là một câu hỏi khó. Alberto Abadie cho rằng bạn nên làm như vậy. Phương pháp ghép cặp linh hoạt hơn, và khi bạn đã có code, việc chạy nó cũng đơn giản như hồi quy tuyến tính. Tôi thì không hoàn toàn bị thuyết phục bởi điều này. Abadie đã từng dành rất nhiều thời gian để nghiên cứu và phát triển mô hình ước lượng này (Abadie là một trong những nhà khoa học đóng góp cho phương pháp ghép cặp để tạo nên nó như ngày nay), vì vậy hiển nhiên Abadie sẽ rất ủng hộ phương pháp này. Thứ hai, có một thứ gì đó trong tính đơn giản của hồi quy tuyến tính mà bạn không thấy trong phương pháp ghép cặp. Phép toán đạo hàm riêng trong đó “các yếu tố khác không thay đổi” của hồi quy tuyến tính dễ nắm bắt hơn phương pháp ghép cặp. Tuy nhiên đây chỉ là quan điểm cá nhân của tôi. Thành thật mà nói, không có một câu trả lời rõ ràng cho vấn đề này. Dù sao đi nữa, hay quay trở lại với ví dụ của chúng ta.

Với công thức điều chỉnh thiên lệch, chúng ta thu được ước lượng ATE.

np.mean((2*predicted["medication"] - 1)*((predicted["recovery"] - predicted["match"])-predicted["bias_correct"]))

-7.36266090614141

Rõ ràng, chúng ta cũng cần phải xác định khoảng tin cậy xung quanh đại lượng này, nhưng lượng kiến thức toán học trong phần này đã quá đủ. Thực tế, chúng ta đơn giản chỉ sử dụng code đã được viết sẵn và chỉ cần dùng câu lệnh import mô hình ước lượng ghép cặp từ thư viện causalinference.

from causalinference import CausalModel

cm = CausalModel(
    Y=med["recovery"].values, 
    D=med["medication"].values, 
    X=med[["severity", "age", "sex"]].values
)

cm.est_via_matching(matches=1, bias_adj=True)

print(cm.estimates)

Treatment Effect Estimates: Matching

                     Est.       S.e.          z      P>|z|      [95% Conf. int.]
--------------------------------------------------------------------------------
           ATE     -7.709      0.609    -12.649      0.000     -8.903     -6.514
           ATC     -6.665      0.246    -27.047      0.000     -7.148     -6.182
           ATT     -9.679      1.693     -5.717      0.000    -12.997     -6.361

Cuối cùng, chúng ta có thể tự tin khẳng định rằng thuốc của chúng ta thực sự làm giảm thời gian hồi phục của người bệnh trong bệnh viện. Ước lượng ATE ở đây nhỏ hơn một chút so với của tôi, vì thế có thể code của tôi chưa thật sự hoàn hảo. Đây cũng là một lý do khác bạn nên sử dụng code đã được viết sẵn thay vì tự viết.

Trước khi chúng ta khép lại chủ đề này, tôi chỉ muốn đề cập tới nguyên nhân của thiên lệch trong phương pháp ghép cặp. Chúng ta đã thấy phương pháp ghép cặp bị thiên lệch khi các cặp được ghép không quá tương tự nhau. Nhưng nguyên nhân nào khiến chúng khác biệt như vậy?

Lời Nguyền Đa Chiều

Hoá ra, câu trả lời khá đơn giản và trực quan. Việc tìm những người có vài điểm tương đồng khá dễ dàng, ví dụ như giới tính. Nhưng nếu chúng ta có nhiều đặc điểm hơn, như tuổi tác, thu nhập, nơi sinh, v.v., việc ghép cặp càng trở nên khó khăn hơn. Một cách tổng quát, càng có nhiều thuộc tính, sự khác biệt giữa đối tượng và đối tượng được ghép với nó sẽ càng cao.

Điều này không đơn giản chỉ làm yếu mô hình ước lượng ghép cặp. Nó cũng liên hệ với mô hình ước lượng phân lớp mà chúng ta đã thấy trước đó. Ban đầu, trong ví dụ về tác dụng của thuốc lên nam và nữ, việc phát triển mô hình ước lượng phân lớp khá dễ vì chúng ta chỉ có duy nhất 2 ô: nam và nữ. Tuy nhiên điều gì sẽ xảy ra nếu chúng ta có nhiều ô hơn? Giả sử chúng ta có 2 biến liên tục là tuổi tác và thu nhập, và chúng ta muốn chia chúng thành 5 nhóm mỗi loại. Vậy là chúng ta sẽ có 25 ô, hay \(5^2\). Vậy nếu chúng ta có 10 biến giải thích với 3 nhóm mỗi loại? Có vẻ là quá nhiều phải không? Chúng ta sẽ có 59049 ô, hay \(3^{10}\). Dễ thấy điều này có thể tăng chóng mặt theo cấp số nhân như thế nào. Đây là một hiện tượng phổ biến trong tất cả các lĩnh vực của khoa học dữ liệu được gọi là **Lời Nguyền Đa Chiều.

Image Source: Deep AI

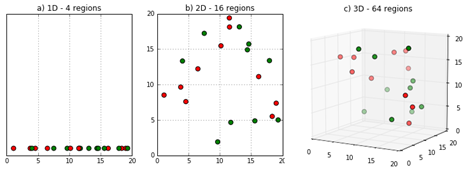
Mặc dù khái niệm này nghe có vẻ nguy hiểm, nó đơn giản là số điểm dữ liệu được yêu cầu để lấp đầy các cột thuộc tính của bộ dữ liệu tăng theo cấp số nhân với số lượng thuộc tính, hay chiều. Vì vậy, nếu có X điểm dữ liệu để lấp đầy 3 cột thuộc tính, thì với 4 cột thuộc tính ta sẽ cần nhiều điểm hơn theo cấp số nhân.

Trong bối cảnh của mô hình ước lượng phân lớp, lời nguyền đa chiều có nghĩa rằng nó sẽ bất lợi nếu có nhiều thuộc tính. Nhiều thuộc tính có nghĩa có nhiều ô X. Nếu có nhiều ô, một vài ô trong số chúng sẽ có rất ít dữ liệu. Một vài thậm chí chỉ có nhóm can thiệp hoặc nhóm đối chứng, vì thế không thể ước lượng ATE, và điều này sẽ làm hỏng mô hình ước lượng của chúng ta. Trong bối cảnh mô hình ước lượng ghép cặp, nó có nghĩa các khoảng thuộc tính sẽ rất rộng và các đối tượng sẽ cách xa nhau. Điều này sẽ làm tăng khoảng cách trong các cặp được ghép và gây ra thiên lệch.

Hồi quy tuyến tính giải quyết vấn đề này khá tốt. Điều nó làm là quy chiếu tất cả các thuộc tính X trong một chiều Y. Sau đó nó so sánh giữa nhóm được can thiệp và nhóm đối chứng trên hệ quy chiếu đó. Như vậy, bằng một cách khác, hồi quy tuyến tính thực hiện giảm chiều dữ liệu để ước lượng ATE.

Hầu hết các mô hình nhân quả cũng có một vài cách để xử lý lời nguyền đa chiều. Tôi sẽ không nhắc lại ở đây nữa, nhưng bạn nên ghi nhớ khi nhìn vào chúng. Khi chúng ta xử lý ví dụ về xu hướng điểm số trong chương sau, hãy cố gắng để tìm ra cách để giải quyết vấn đề này.

Ý tưởng chủ đạo

Chúng ta đã bắt đầu chương này bằng cách hiểu về hồi quy tuyến tính và làm cách nào nó có thể giúp chúng ta xác định các quan hệ nhân quả. Cụ thể, chúng ta thấy hồi quy có thể được xem như việc chia bộ dữ liệu thành các ô, tính toán ATE trong từng ô và sau đó kết hợp tất cả các ô ATE lại thành một ATE duy nhất cho toàn bộ dữ liệu.

Từ đó, chúng ta suy ra một mô hình ước lượng nhân quả tổng quát với phân lớp. Chúng ta đã thấy tại sao mô hình ước lượng này không quá hữu dụng trong thực tế nhưng cung cấp cho chúng ta cách nhìn thú vị về cách giải quyết vấn đề ước lượng suy luận nhân quả. Điều này tạo cơ hội cho chúng ta đề cập tới mô hình ước lượng ghép cặp.

Ghép cặp kiểm soát biến nhiễu bằng cách nhìn vào mỗi đối tượng được can thiệp và ghép cặp đối chứng tương tự với nó, và sau đó làm tương tự với đối tượng đối chứng. Chúng ta thấy cách thực hiện phương pháp này sử dụng thuật toán KNN và cách để loại bỏ thiên lệch sử dụng hồi quy tuyến tính. Cuối cùng, chúng ta thảo luận sự khác biệt giữa ghép cặp và hồi quy tuyến tính. Chúng ta thấy cách ghép cặp là một mô hình ước lượng phi tham số không phụ thuộc vào tuyến tính như hồi quy tuyến tính.

Cuối cùng, chúng tôi đi sâu vào vấn đề dữ liệu nhiều chiều và thấy cách các phương pháp suy luận nhân quả có thể bị ảnh hưởng bởi nó.

Tài liệu tham khảo

Tôi muốn dành loạt bài viết này để vinh danh Joshua Angrist, Alberto Abadie and Christopher Walters vì khóa học Kinh tế lượng tuyệt cú mèo của họ. Phần lớn ý tưởng trong loạt bài này được lấy từ các bài giảng của họ được tổ chức bởi Hiệp hội Kinh tế Mĩ. Theo dõi các bài giảng này là những gì tôi làm trong suốt năm 2020 khó nhằn.

• Kinh tế lượng với dữ liệu chéo
• Luyện chưởng Kinh tế lượng Gần như Vô hại

Tôi cũng muốn giới thiệu cuốn sách lý thú của Angrist. Chúng cho tôi thấy Kinh tế lượng, hoặc ‘Lượng theo cách họ gọi không chỉ vô cùng hữu ích mà còn rất vui.

• Kinh tế lượng Gần như Vô hại
• Luyện chưởng ‘Lượng’

Tài liệu tham khảo cuối cùng của tôi là cuốn sách của Miguel Hernan and Jamie Robins. Nó là người bạn đồng hành tin cậy với tôi khi trả lời những câu hỏi nhân quả khó nhằn.

• Sách Suy Luận Nhân Quả

Bảng Từ Viết tắt

Viết tắt	Tiếng Anh	Tiếng Việt
ATE	Average Treatment Effect	Tác động Can thiệp Trung bình
ATET	Average Treatment Effect on the Treated	Tác động Can thiệp Trung bình trên Nhóm được Can thiệp
KNN	K Nearest Neighbour	K Láng giềng Gần nhất
LATE	Local Average Treatment Effect	Tác động Can thiệp Bình quân Cục bộ

Bảng Thuật ngữ

Thuật ngữ	Tiếng Anh
biến giả	dummy, dummy variable
biến giải thích	covariate
biến liên tục	continuous variable
biến nhiễu	confounder, confounding variable
biến phụ thuộc	dependent variable
bình quân gia quyền	weighted average
bộ dữ liệu	dataset
có tham số	parametric
dữ liệu	data
ghép cặp	matching
giá trị trung bình	mean
giả thiết	assumption
giảm chiều dữ liệu	dimensionality reduction
hiệu của các giá trị trung bình	mean difference
hồi quy	regression, regress
hồi quy tuyến tính	linear regression
k láng giềng gần nhất	k nearest neighbour
khoa học dữ liệu	data science
khoảng cách	proximity
khoảng cách euclid	euclidean norm
khoảng tin cậy	confidence interval
kích thước mẫu	sample size
kết quả	outcome
kết quả giả tưởng	counterfactual outcome
láng giềng gần nhất	nearest neighbour
lời nguyền đa chiều	curse of dimensionality
mô hình nhân quả	causal model
mô hình ước lượng	estimator
mô hình ước lượng ghép cặp	matching estimator
mô hình ước lượng phân lớp	subclassification estimator
mẫu	sample
ngoại suy	extrapolation, extrapolate
nhiễu	confounding
nhóm can thiệp	treated group
nhóm được can thiệp	treatment group, test group
nhóm đối chứng	control group, untreated group
ols	ols
phi tham số	non-parametric
phi tuyến tính	non linearity
phân lớp	subclassification
phân phối chuẩn	normal distribution
phương sai	variance
quan hệ nhân quả	causality, causation, causal relationship
quan sát	observe, observation
quy luật tạo lập dữ liệu	data generating process
suy luận nhân quả	causal inference, causal reasoning
thiên lệch	bias
thiên lệch ghép cặp	matching bias
thuật toán	algorithm
thuộc tính	feature
tuyến tính	linearity, linear
tác động	impact
tác động can thiệp	treatment effect, treatment impact
tập huấn luyện	training set
điều chỉnh thiên lệch	bias correction
được can thiệp	treated
đạo hàm riêng	partial derivative
định luật giới hạn trung tâm	central limit theorem
đối chứng	untreated, non-treated
độc lập có điều kiện	conditionally independent, conditional independence