Sự bất tuân và LATE

SUY LUẬN NHÂN QUẢ VỚI PYTHON - KỲ 9

Bài viết này thuộc chuỗi bài viết về “Suy luận Nhân quả với Python”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây

Để hiểu một cách trực quan về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “60 Giây Nhân quả” tại đây

Nhón chân vào Thế giới dị biệt

Nhiều hiểu biết sâu sắc về việc áp dụng IV (Instrumental Variable) hiện đại được rút ra từ y học. Nhìn chung nó phân chia bốn loại đối tượng phụ thuộc vào cách phản ứng với biến công cụ.

1. Người tuân thủ
2. Người luôn không nhận
3. Người luôn nhận
4. Người chống đối

Cách đặt tên này xuất phát từ dược học. Hãy tưởng tượng bạn đang tiến hành một thử nghiệm để kiểm tra tác dụng của một loại thuốc mới đối với một vài loại bệnh. Mỗi đối tượng được chỉ định một phương pháp điều trị: thuốc hoặc giả dược. Người tuân thủ là những đối tượng nghe theo chỉ định. Nếu họ được chỉ định dùng giả dược, họ dùng giả dược; nếu họ được chỉ định dùng thuốc, họ dùng thuốc. Người luôn không nhận là những đối tượng từ chối dùng thuốc. Ngay cả khi họ được chỉ định dùng loại thuốc mới, họ cũng sẽ không sử dụng chúng. Mặt khác, người luôn nhận là những người mà bằng một cách nào đó luôn lấy được thuốc mới cho dù họ được chỉ định dùng giả dược. Cuối cùng, người chống đối là những người nhận điều trị nếu được chỉ định vào nhóm đối chứng và không nhận điều trị nếu được chỉ định điều trị. Hay nói cách khác, người chống đối là nhóm luôn làm trái với chỉ định. Trong thực tế, nhóm này không quá phổ biến nên chúng ta thường bỏ qua.

IV hiện đại coi biến công cụ như một thiết kế bán can thiệp mà tính tuân thủ không đạt mức hoàn hảo. Do đó nó phân biệt tính nội suy và tính ngoại suy của tác động nhân quả. Xin nhắc lại, một tác động có tính nội suy là một tác động mà chúng ta có thể xác định. Nó phù hợp trong một hoàn cảnh cụ thể với dữ liệu cụ thể. Trong trường hợp IV, nó là tác động can thiệp đối với những đối tượng mà biến công cụ làm thay đổi sự can thiệp. Mặt khác, tính ngoại suy lại liên quan đến khả năng dự đoán của tác động nhân quả. Một câu hỏi sẽ được đưa ra là liệu chúng ta có nên khái quát hoát tác động mà chúng ta tìm thấy đối với các mẫu khác hay không. Ví dụ, giả sử bạn đang thực hiện một RCT trong trường đại học để tìm hiểu xem mọi người có hào phóng hay không khi họ nhận được một phần thưởng nếu làm từ thiện. Thử nghiệm được thiết kế tốt, tuy nhiên bạn chỉ mời những sinh viên ngành kinh tế tham gia. Sau đó bạn nhận thấy rằng tất cả họ đều là những kẻ ích kỷ. Đó là một kết luận có tính nội suy. Nó phù hợp cho những điểm dữ liệu đó. Tuy nhiên, từ thử nghiệm này, liệu bạn có thể suy ra rằng loài người là một giống loài ích kỷ? Điều này gần như không thể xảy ra. Vì thế chúng ta đặt ra câu hỏi liệu thử nghiệm của bạn có tính ngoại suy để khái quát hoá kết qủa thử nghiệm hay không. Dù sao đi nữa, hãy quay trở lại với IV.

Trong một ví dụ cụ thể hơn, xem xét trường hợp bạn muốn tăng lượng người dùng tương tác được đo bằng lượng mua trong ứng dụng. Một cách để làm điều này là bạn có thể yêu cầu bộ phận marketing đưa ra một gói khuyến mại để thu hút khách hàng. Bộ phận marketing cho ra mắt một thiết kế ấn tượng với giao diện tương tác hấp dẫn. Với chiến lược này, bạn chuyển sang thiết kế một thử nghiệm ngẫu nhiên. Bạn chọn ngẫu nhiên 10.000 khách hàng, với xác suất mỗi người nhận được gói khuyến mại là 50%. Tuy nhiên, khi tiến hành thử nghiệm, bạn nhận ra có một số khách hàng được chỉ định nhận gói khuyến mại nhưng thực tế lại không nhận được. Khi trao đổi với các kỹ sư lập trình, họ cho rằng có thể do khách hàng sử dụng điện thoại đời cũ nên không được hỗ trợ cài đặt gói khuyến mại nhóm marketing đã thiết kế.

Lúc đầu, bạn có thể cho rằng đây không phải là vấn đề đáng lo ngại. Thay vì sử dụng chỉ định can thiệp làm biến can thiệp, bạn có thể sử dụng biến tiếp nhận can thiệp phải không? Tuy nhiên, vấn đề hoá ra không đơn giản như vậy. Nếu nhìn vào biểu đồ nhân quả của toàn bộ tình huống này, bạn sẽ thấy:

import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np
from scipy import stats
from matplotlib import style
import seaborn as sns
from matplotlib import pyplot as plt
import statsmodels.formula.api as smf
from linearmodels.iv import IV2SLS
import graphviz as gr

%matplotlib inline

style.use("fivethirtyeight")

g = gr.Digraph()

g.edge("chỉ định", "tiếp nhận")
g.edge("tiếp nhận", "lượng mua")
g.edge("thu nhập", "lượng mua")
g.edge("thu nhập", "tiếp nhận")
g.node("thu nhập", color="blue")
g

Theo biểu đồ nhân quả, bạn là người chỉ định gói khuyến mại (push assigned). Việc chỉ định được thiết kế ngẫu nhiên nên không có yếu tố chi phối. Sau đó, bạn có một đỉnh về việc tiếp nhận gói khuyến mại (push delivered). Không phải tất cả những người được chỉ định gói khuyến mại đều tiếp nhận nó, vì thế ở đây xuất hiện sự không tuân thủ (hay sự bất tuân). Cụ thể hơn, có một vài người luôn không nhận: những người không nhận sự can thiệp ngay cả khi họ được chỉ định. Bạn có lý do để nghi ngờ rằng sụ không tuân thủ này không đơn giản là do tình cờ. Bởi vì những người sử dụng điện thoại đời cũ hơn thì không nhận được gói khuyến mại, bạn có thể lập luận rằng thu nhập của khách hàng cũng chi phối sự tiếp nhận gói khuyến mại. Cuối cùng, bạn thu được biến kết quả, lượng mua trong ứng dụng (in app purchase). Nhớ rằng chúng ta không hề biết thu nhập (income) của khách hàng, vì thế chúng ta không thể kiểm soát biến này. Với những lập luận này, hãy cùng kiểm tra xem điều gì sẽ xảy ra nếu chúng ta chỉ sử dụng việc chỉ định gói khuyến mại làm biến can thiệp, cũng như chỉ sử dụng việc tiếp nhận gói khuyến mại làm biến can thiệp.

Trong trường hợp đầu tiên, chúng ra sẽ ước lượng tác động nhân quả bằng hiệu số giữa các giá trị trung bình:

\[ATE = E[Y | chỉ định=1] - E[Y | chỉ định=0]\]

Như chúng ra đã biết, đây chỉ là ước lượng không thiên lệch cho \(E[Y_1] - E[Y_0]\) nếu thiên lệch \(E[Y_0|chỉ định=0] - E[Y_0|chỉ định=1]\) bằng 0. Bởi vì chỉ định là ngẫu nhiên, chúng ta biết rằng thiên lệch bằng 0. Liệu điều này đã giải quyết vấn đề chưa? Không hẳn. Nếu chúng ta làm như vậy, chúng ta thực ra đang đi trả lời cho một câu hỏi khác với câu hỏi ban đầu. Chúng ta sẽ đi tìm tác động nhân quả của sự chỉ định can thiệp, chứ không phải của sự can thiệp. Nhưng liệu những điều này có khác nhau và liệu chúng ta có thể ngoại suy tác động nhân quả của sự chỉ định can thiệp lên ATE? Hay nói cách khác, liệu tác động nhân quả của sự chỉ định can thiệp có là ước lượng không thiên lệch của ATE?

Hoá ra không phải vậy. Vì có không tuân thủ, kết quả của những người được chỉ định can thiệp sẽ bị thiên về hướng giống với kết quả của những người trong nhóm đối chứng. Không tuân thủ sẽ đảo ngược sự can thiệp một cách ngoài ý muốn, làm cho kết quả của nhóm được can thiệp và nhóm đối chứng tương tự nhau hơn. Đừng nhầm lẫn điều này với sự tương tự giữa các biến. Chúng ta mong muốn các biến trong nhóm được can thiệp và nhóm đối chứng tương đương hay tương đồng. Điều chúng ta không mong muốn xảy ra là chúng sẽ có kết quả tương tự nhau nếu thực sự có tác động can thiệp.

Để hiểu rõ điểm này, giả sử ban đầu trong những người luôn nhận, một số được chỉ định vào nhóm đối chứng một cách ngẫu nhiên. Tuy nhiên những người này, bằng một cách nào đó, luôn nhận can thiệp. Do đó về bản chất họ là những người nhận can thiệp bị lẫn trong nhóm đối chứng. Hậu quả là, việc xác định tác động nhân quả trở nên khó khăn hơn khi xuất hiện không tuân thủ.

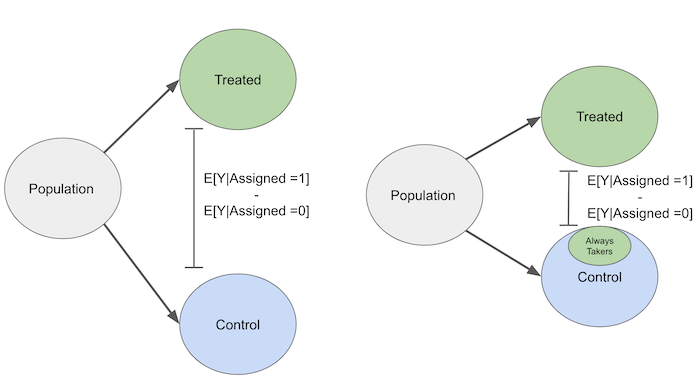
Với cùng lập luận, những người luôn không nhận sẽ làm cho những người được chỉ định can thiệp trông như những người không được can thiệp. Theo cách này, tác động nhân quả của sự chỉ định can thiệp thiên lệch về 0. Một cách khác để xem xét trường hợp này là tưởng tượng ra một trường hợp cực đoan. Giả sử rằng không tuân thủ rất cao, vì vậy sự chỉ định can thiệp không đưa ra được thông tin gì về can thiệp nhận được (theo IV, có thể nói rằng chúng ta có bước 1 rất kém). Sử dụng Z để ký hiệu cho sự chỉ định can thiệp, chúng ta có:

\[E[Y|Z=1] - E[Y|Z=0] = 0\]

Điều này là bởi không có liên kết nhân quả giữa chỉ định can thiệp và kết quả. Z chỉ là một biến ngẫu nhiên vô nghĩa.

g = gr.Digraph()

g.node("chỉ định")
g.edge("tiếp nhận", "lượng mua")
g.edge("thu nhập", "lượng mua")
g.edge("thu nhập", "tiếp nhận")
g.node("thu nhập", color="blue")
g

OK, vậy là chúng ta đã loại bỏ việc sử dụng tác động nhân quả của chỉ định để ước lượng tác động nhân quả của can thiệp. Vậy làm thế nào chỉ dùng sự tiếp nhận can thiệp?

\[ATE = E[Y | tiếp nhận=1] - E[Y | tiếp nhận=0]\]

Một lần nữa, chúng ta cần suy nghĩ liệu điều này có bị thiên lệch hay không, hoặc nếu như \(E[Y_0|tiếp nhận=0] = E[Y_0|tiếp nhận=1]\). Chỉ bằng việc nhìn vào biểu đồ nhân quả phía trên, chúng ta biết rằng những điều này không thể xảy ra. Chúng ta có biến nhiễu không đo lường được (thu nhập) đang “rình rập” xung quanh và chắc chắn sẽ làm rối tung hết mọi thứ lên. Như đã nói từ trước, chúng ta biết rằng sự thất bại trong việc phân phối gói khuyến mại, trong trường hợp của chúng ta, gây ra bởi việc khách hàng sử dụng điện thoại đời cũ. Điều này có nghĩa rằng chúng ta có thể có \(E[Y_0|tiếp nhận=0] < E[Y_0|tiếp nhận=1]\). Chúng ta nghĩ rằng trường hợp này có thể xảy ra bởi những khách hàng có thu nhập thấp hơn thì sử dụng điện thoại đời cũ hơn dẫn đến \(tiếp nhận=0\) và cũng có ít khả năng sử dụng tính năng mua trong ứng dụng \(Y_0\).

Vậy là chúng ta không thể sử dụng cả chỉ định can thiệp và tiếp nhận can thiệp để ước lượng ATE. May mắn thay, chúng ta vẫn có thể sử dụng: Biến Công Cụ. Ở đây, chỉ định can thiệp là biến công cụ hoàn hảo cho sự can thiệp. Nó có tính ngẫu nhiên và chỉ tác động đến việc mua trong ứng dụng thông qua sự can thiệp.

Tác Động Can Thiệp Bình Quân Cục Bộ: LATE

Tác động can thiệp bình quân cục bộ làm rõ tổng thể mà chúng ta có thể ước lượng tác động nhân quả. Nó cũng là một cách khác để nhìn nhận IV, đưa ra một cách giải thích lý thú về mặt trực giác mà chúng ta có thể vận dụng. Trong IV hiện đại, chúng ta coi biến công cụ như điểm xuất phát cho chuỗi nhân quả: Z gây ra T, T gây ra Y. Trong bối cảnh này, điều kiện loại trừ nghĩa là Z không chi phối Y ngoài kênh tác động lên T. 1St stage được xem là tác động nhân quả của Z lên T. Chúng ta cũng ký hiệu các kết quả tiềm năng với hai chỉ số, trong đó chỉ số đầu ký hiệu sự giả tưởng cho biến công cụ và chỉ số thứ hai cho sự can thiệp

\[\text{Kết quả tiềm năng}=\begin{cases} Y_i(1, 1) \ \text{nếu } T_i=1, \ Z_i=1\\ Y_i(1, 0) \ \text{nếu } T_i=1, \ Z_i=0\\ Y_i(0, 1) \ \text{nếu } T_i=0, \ Z_i=1\\ Y_i(0, 0) \ \text{nếu } T_i=0, \ Z_i=0\\ \end{cases}\]

Theo cách này, sự can thiệp trở thành kết quả, ít nhất trong bước 1. Điều này có nghĩa rằng chúng ta cũng có thể sử dụng ký hiệu để biểu diễn kết quả tiềm năng:

\[\text{Can thiệp tiềm năng}=\begin{cases} T_0 \ \text{nếu } Z_i=0 \\ T_1 \ \text{nếu } Z_i=1 \end{cases}\]

Giả thiết về Biến Công Cụ có thể được viết lại dưới dạng sau:

1. \(T_{i0}, T_{i1} \perp Z_i \) và \(Y_i(T_{i1},1), Y_i(T_{i0},0) \perp Z_i \). Đây là giả thiết về tính độc lập. Nó có nghĩa biến công cụ được chỉ định ngẫu nhiên. Hay nói cách khác, Z, biến công cụ, không tương quan với các can thiệp tiềm năng, đồng nghĩa với việc những đối tượng trong những nhóm biến công cụ khác nhau là tương đồng.

2. \(Y_i(1, 0)=Y_i(1, 1)=Y_{i1}\) và \(Y_i(1, 0)=Y_i(1, 1)=Y_{i0}\). Đây là điều kiện loại trừ. Nó cho thấy nếu chúng ta đang xem xét các kết quả tiềm năng cho nhóm được can thiệp thì cả hai nhóm biến công cụ như nhau. Nói cách khác, biến công cụ không tác động lên kết quả tiềm năng, đồng nghĩa với việc biến công cụ chỉ tác động lên kết quả thông qua sự can thiệp.

3. \(E[T_{i1}-T_{i0}] \neq 0\). Giả thiết này nói về sự tồn tại của bước 1. Nó cho thấy kết quả tiềm năng của bước 1, hay can thiệp tiềm năng, không giống nhau. Hay nói cách khác biến công cụ tác động lên sự can thiệp.

4. \(T_{i1} > T_{i0}\). Đây là giả thiết về tính đơn điệu. Nó cho thấy nếu tất cả mọi người đều có biến công cụ, mức độ can thiệp sẽ cao hơn nếu tất cả mọi người “tắt” công cụ.

Hãy cùng ôn lại kiến thức về mô hình ước lượng Wald để hiểu hơn về IV:

\[ATE = \dfrac{E[Y|Z=1]-E[Y|Z=0]}{E[T|Z=1]-E[T|Z=0]}\]

Hãy xem xét phần đầu tiên của công thức này, \(E[Y|Z=1]\). Sử dụng điều kiện loại trừ, chúng ta có thể biểu diễn Y theo kết quả tiềm năng như sau.

\[E[Y_i|Z_i=1]=E[Y_{i0} + T_{i1}(Y_{i1} - Y_{i0})|Z=1]\]

Sử dụng tính chất độc lập, chúng ta có thể loại bỏ điều kiện trên Z

\[E[Y_i|Z_i=1]=E[Y_{i0} + T_{i1}(Y_{i1} - Y_{i0})]\]

Tương tự, chúng ta thu được

\[E[Y_i|Z_i=0]=E[Y_{i0} + T_{i0}(Y_{i1} - Y_{i0})]\]

Chúng ta có thể biểu diễn tử số của mô hình ước lượng Wald như sau

\[E[Y|Z=1]-E[Y|Z=0] = E[(Y_{i1}-Y_{i0})(T_{i1}-T_{i0})]\]

Sử dụng tính chất đơn điệu, chúng ta biết rằng \(T_{i1}-T_{i0}\) bằng 0 hoặc 1, vì vậy

\[E[(Y_{i1}-Y_{i0})(T_{i1}-T_{i0})]\] \[= E[(Y_{i1}-Y_{i0})|T_{i1}>T_{i0}]P(T_{i1}>T_{i0})\]

Tương tự với mẫu số của mô hình ước lượng Wald, ta cũng có

\[E[T|Z=1]-E[T|Z=0]=E[T_{i1}-T_{i0}]=P(T_{i1}>T_{i0})\]

Từ tất cả các phương trình trên, chúng ta có thể biểu diễn mô hình ước lượng Wald như sau:

\[ATE = \dfrac{E[(Y_{i1}-Y_{i0})|T_{i1}>T_{i0}]P(T_{i1}>T_{i0})}{P(T_{i1}>T_{i0})}\] \[=E[(Y_{i1}-Y_{i0})|T_{i1}>T_{i0}]\]

Công thức này có nghĩa ATE được ước lượng bởi IV là ATE trong mẫu với \(T_{i1}>T_{i0}\). Và nếu bạn suy ngẫm về tính tuân thủ, tổng thể ở đây là gì? Đó là tổng thể mà những người có biến công cụ có mức can thiệp cao hơn nếu họ không có biến công cụ. Hay nói cách khác, đây là tổng thể người tuân thủ. Để chúng ta có thể nhớ rõ hơn,

1. Người tuân thủ nghĩa là \(T_{i1}>T_{i0}\)
2. Người Luôn Không Nhận \(T_{i1}=T_{i0}=0\)
3. Người Luôn Nhận \(T_{i1}=T_{i0}=1\)

Tóm lại, IV không cung cấp thông tin gì về tác động lên người luôn không nhận, người luôn nhận, hay người chống đối, bởi sự can thiệp không thay đổi đối với những đối tượng này! IV chỉ tìm tác động can thiệp cho những người tuân thủ.

Tác động lên sự tương tác

Hãy cùng xem tất cả những điều trên đóng vai trò như thế nào trong trường hợp chúng ta đang ước lượng tác động của gói khuyến mại lên lượng mua trong ứng dụng. Chúng ta đã có một biểu đồ nhân quả phía trên, vì vậy chúng ta sẽ không biểu thị lại đồ thị này ở đây nữa. Dữ liệu chúng ta có bao gồm sự chỉ định gói khuyến mại (biến công cụ ngẫu nhiên) và sự tiếp nhận gói khuyến mại (biến can thiệp).

data = pd.read_csv("./data/app_engagement_push.csv").rename(columns=dict(in_app_purchase='lượng_mua',
                                                         push_assigned='chỉ_định',
                                                         push_delivered='tiếp_nhận'))
    
data.head()

	lượng_mua	chỉ_định	tiếp_nhận
0	47	1	1
1	43	1	0
2	51	1	1
3	49	0	0
4	79	0	0

Đầu tiên, hãy chạy OLS để xem chúng ta có thể thu được kết quả như thế nào.

ols = IV2SLS.from_formula("lượng_mua ~ 1 + chỉ_định + tiếp_nhận", data).fit()
ols.summary.tables[1]

Parameter Estimates

	Parameter	Std. Err.	T-stat	P-value	Lower CI	Upper CI
Intercept	69.292	0.3624	191.22	0.0000	68.581	70.002
chỉ_định	-17.441	0.5702	-30.590	0.0000	-18.559	-16.324
tiếp_nhận	27.600	0.6124	45.069	0.0000	26.399	28.800

OLS cho thấy tác động can thiệp là 27.60, có nghĩa là gói khuyến mại tăng lượng mua trong ứng dụng thêm 27.6 reais (đơn vị tiền tệ của Brazil). Tuy nhiên, chúng ta có lý do để nghi ngờ rằng đây là một ước lượng chệch. Chúng ta biết rằng những điện thoại cũ hơn gặp khó khăn trong việc nhận gói khuyến mại, vì vậy có thể những khách hàng giàu có hơn với điện thoại mới hơn là những người tuân thủ. Bởi vì những người nhận can thiệp thì có nhiều tiền hơn, chúng ta tin rằng đây là thiên lệch dương và tác động thật sự của gói khuyến mại thấp hơn. Nói cách khác, chúng ta có thể có \(E[Y_0|T=0] < E[Y_0|T=1]\).

Hãy thử ước lượng tác động này với Biến Công Cụ. Đầu tiên, hãy chạy bước 1.

first_stage = IV2SLS.from_formula("tiếp_nhận ~ 1 + chỉ_định", data).fit()
first_stage.summary.tables[1]

Parameter Estimates

	Parameter	Std. Err.	T-stat	P-value	Lower CI	Upper CI
Intercept	-1.11e-16	1.815e-10	-6.118e-07	1.0000	-3.557e-10	3.557e-10
chỉ_định	0.7176	0.0064	112.07	0.0000	0.7050	0.7301

Có vẻ như chúng ta có bước 1 tốt. Có 71.8% người nhận được gói khuyến mại trong tổng số những người được chỉ định nhận gói khuyến mại. Điều này cũng có nghĩa rằng chúng ta có khoảng 28% những người luôn không nhận. Chúng ta cũng có lý do chắc chắn để khẳng định rằng không có người luôn nhận bởi tham số hệ số chặn được ước lượng bằng 0. Có nghĩa rằng không ai nhận gói khuyến mại nếu không được chỉ định. Điều này có thể dự đoán được trong phạm vi thiết kế thử nghiệm của chúng ta.

Hãy chạy dạng tối giản:

reduced_form = IV2SLS.from_formula("lượng_mua ~ 1 + chỉ_định", data).fit()
reduced_form.summary.tables[1]

Parameter Estimates

	Parameter	Std. Err.	T-stat	P-value	Lower CI	Upper CI
Intercept	69.292	0.3624	191.22	0.0000	68.581	70.002
chỉ_định	2.3636	0.5209	4.5376	0.0000	1.3427	3.3845

Dạng tối giản cho thấy rằng tác động nhân quả của chỉ định can thiệp là 2.36. Có nghĩa rằng chỉ định một người nào đó nhận gói khuyến mại làm tăng lượng mua trong ứng dụng thêm 2.36 reais.

Nếu chúng ta chia dạng tối giản cho bước 1, chúng ta chia tác động của biến công cụ cho các đơn vị can thiệp, thu được \(2.3636/0.7176=3.29\). Chạy 2SLS, chúng ta thu được ước lượng tương tự, với sai số chuẩn thích hợp.

iv = IV2SLS.from_formula("lượng_mua ~ 1 + [tiếp_nhận ~ chỉ_định]", data).fit()
iv.summary.tables[1]

Parameter Estimates

	Parameter	Std. Err.	T-stat	P-value	Lower CI	Upper CI
Intercept	69.292	0.3624	191.22	0.0000	68.581	70.002
tiếp_nhận	3.2938	0.7165	4.5974	0.0000	1.8896	4.6981

Kết quả sử dụng 2SLS thu được thấp hơn nhiều so với kết quả sử dụng OLS: 3.29 so với 27.60. Điều này hợp lý bởi tác động nhân quả ước lượng bởi OLS chệch dương. Chúng ta cũng cần phải nhắc lại về LATE. 3.29 là tác động nhân quả trung bình lên những người tuân thủ. Đáng tiếc rằng chúng ta không thể khẳng định bất cứ điều gì về những người luôn không nhận. Có nghĩa rằng chúng ta đang ước lượng tác động lên phân khúc khách hàng giàu hơn của tổng thể, những người sử dụng điện thoại đời mới hơn.

Ý tưởng chủ đạo

Trong chương này, chúng ta đã xem xét một cách nhìn mới hơn về Biến Công Cụ. Chúng ta đã thấy làm thế nào mà IV được coi như một mắt xích trong chuỗi nhân quả, biến công cụ gây ra sự can thiệp, và sự can thiệp lại gây ra kết quả. Theo cách nhìn này, chúng ta đã xem xét tính tuân thủ để hiểu về ATE trong ước lượng IV, và chúng ta khám phá ra nó chính là LATE của những người tuân thủ.

Tài liệu tham khảo

Tôi muốn dành loạt bài viết này như lời cảm ơn tới Joshua Angrist, Alberto Abadie và Christopher Walters bởi lớp học Kinh tế lượng tuyệt vời của họ. Hầu hết những ý tưởng trong chương này được đúc kết từ những bài giảng của họ tại Hiệp hội kinh tế Hoa Kỳ. Lắng nghe các bài giảng của họ giúp tôi có thêm động lực đi qua một năm 2020 đầy khó khăn này.

• Kinh tế lượng với dữ liệu chéo
• Luyện chưởng Kinh tế lượng gần như vô hại

Tôi cũng trích dẫn một cuốn sách tuyệt vời từ Angrist. Họ đã thành công trong việc chỉ cho tôi thấy rằng Kinh tế lượng, hoặc là Lượng theo cách gọi của họ, không chỉ cực kỳ hữu ích mà còn vô cùng thú vị.

• Kinh tế lượng gần như vô hại
• Luyện chưởng ‘Lượng’

Cuối cùng, không thể không nhắc đến cuốn sách được viết bởi Miguel Hernan và Jamie Robins. Nó là người bạn đồng hành đáng tin cậy giúp tôi tìm lời giải đáp cho những câu hỏi hóc búa nhất về tính nhân quả.

• Sách Suy luận nhân quả

Bảng Từ Viết tắt

Viết tắt	Tiếng Anh	Tiếng Việt
2SLS	Two-Stage least square	Bình phương Tối thiểu Hai bước
ATE	Average Treatment Effect	Tác động Can thiệp Trung bình
IV	Instrumental Variable	Biến Công cụ
LATE	Local Average Treatment Effect	Tác động Can thiệp Bình quân Cục bộ
RCT	Randomized Controlled Trial	Thử nghiệm Ngẫu nhiên Đối chứng

Bảng Thuật ngữ

Thuật ngữ	Tiếng Anh
biến công cụ	instrumental-variable, instrumental variable, instrument, instrument variable
biến kết quả	outcome variable
biến nhiễu	confounder, confounding variable
bước 1	1st-stage, first stage, 1st stage
can thiệp tiềm năng	potential treatment
chệch	biased
dạng tối giản	reduced form, reduced-form
dữ liệu	data
giá trị trung bình	mean
giả thiết	assumption
giả tưởng	counterfactual
hệ số chặn	intercept
không thiên lệch	unbiased
kết quả	outcome
kết quả tiềm năng	potential outcome
mô hình ước lượng	estimator
mẫu	sample
ngoại suy	extrapolation, extrapolate
nhóm được can thiệp	treatment group, test group
nhóm đối chứng	control group, untreated group
ols	ols
sai số chuẩn	standard error
thiên lệch	bias
thiết kế bán can thiệp	quasi-experimental design
tuân thủ	compliance
tác động can thiệp	treatment effect, treatment impact
tác động can thiệp bình quân cục bộ	local average treatment effect
tác động nhân quả trung bình	average causal effect
tính ngoại suy	external validity
tính nội suy	internal validity
tương quan	correlate
tổng thể	population
điều kiện loại trừ	exclusion restriction
được can thiệp	treated
đỉnh	node