Sai khác của Biến thiên
SUY LUẬN NHÂN QUẢ VỚI PYTHON - KỲ 14
Bài viết này thuộc chuỗi bài viết về “Suy luận Nhân quả với Python”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây
Để hiểu một cách trực quan về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “60 Giây Nhân quả” tại đây
Ba Biển Quảng cáo ngoài trời ở Nam Brazil
Tôi nhớ lại khoảng thời gian làm marketing (tiếp thị). Khi ấy một kênh tuyệt cú mèo là marketing trực tuyến. Nó không chỉ hiệu quả, mà còn rất thuận tiện để đánh giá tính hiệu quả. Với marketing trực tuyến, bạn có cách để nhận biết khách hàng nào đã xem quảng cáo và theo dõi bằng cookies để xem họ có ghé thăm trang web điều hướng hay không. Bạn cũng có thể sử dụng học máy để tìm đối tượng mục tiêu tương tự các khách hàng của bạn và phát quảng cáo đến họ. Tóm lại, marketing trực tuyến rất hiệu quả: bạn nhắm đến những đối tượng bạn muốn và bạn có thể theo dõi xem họ có hồi đáp theo cách mà bạn mong muốn hay không.
Nhưng không phải ai cũng là đối tượng của makerting trực tuyến. Đôi khi bạn phải sử dụng những phương pháp kém chính xác hơn như quảng cáo TV hoặc đặt các biển quảng cáo ngoài trời trên đường phố. Nhiều khi việc đa dạng hóa kênh marketing là điều mà các phòng marketing hướng đến. Nhưng nếu marketing trực tuyến là cần câu chuyên nghiệp để săn một loại cá ngừ cụ thể, biển quảng cáo và TV là những tấm lưới lớn bạn quăng ra đón cả bầy cá và hi vọng sẽ tóm được một vài con ngon. Nhưng một vấn đề khác với biển quảng cáo và quảng cáo TV là rất khó đánh giá tính hiệu quả của chúng. Bạn chắc chắn có thể đo được lượng mua hàng hoặc bất kì chỉ tiêu nào khác, trước và sau khi đặt biển quảng cáo ở đâu đó. Giả sử có sự gia tăng trong các chỉ tiêu này, liệu đó có phải bằng chứng cho tính hiệu quả của chương trình marketing? Nhưng bạn có chắc sự gia tăng đó không phải xu hướng tăng trưởng tự nhiên trong nhận thức của công chúng về sản phẩm của bạn. Hay nói cách khác, làm thể nào để bạn biết giả tưởng \(Y_0\), điều lẽ ra xảy đến nếu bạn không đặt biển quảng cáo?

Một kĩ thuật dùng để trả lời những loại câu hỏi này là Sai khác của biến thiên. Sai khác của biến thiên thường được dùng để đánh giá tác động của các can thiệp vĩ mô, như tác động của nhập cư đối với thất nghiệp, tác động của thay đổi luật quản lý súng và tỉ lệ tội phạm hoặc đơn giản là khác biệt trong lượng tương tác người dùng do một chiến dịch marketing. Trong tất cả các trường hợp này, bạn phải có một khoảng thời gian trước và sau can thiệp và mong muốn tách biệt tác động của can thiệp khỏi xu hướng vận động chung. Một ví dụ cụ thể, hãy cùng xem xét một câu hỏi tương tự như điều mà tôi đã từng phải trả lời.
Để đánh giá xem các biển quảng cáo có phải là một kênh marketing hiệu quả hay không, chúng tôi đã đặt 3 biển quảng cáo ở thành phố Porto Alegre, thủ phủ bang Rio Grande do Sul. Dành cho những người không quen thuộc với địa lý Brazil, miền nam của nước này là một trong những vùng phát triển nhất với tỉ lệ đói nghèo thấp nếu so sánh với phần còn lại. Nắm được điều này, chúng tôi đã quyết định nhìn vào dữ liệu từ Florianopolis, thủ phủ của bang Santa Catarina, một bang khác ở miền nam. Ý tưởng là chúng tôi sẽ sử dụng Florianopolis làm mẫu đối chứng để ước lượng giả tưởng \(Y_0\). Chỉ tiêu chúng tôi cố thúc đẩy ở chiến dịch này là lượng tiền gửi vào tài khoản tiết kiệm (Các mô tả dưới đây không phỉa thí nghiệm thực tế, vì nó cần được bảo mật, nhưng ý tưởng khá tương tự). Chúng tôi đã đặt biển quảng cáo ở Porto Alegre trong suốt tháng 6. Dữ liệu chúng tôi thu được có dạng như sau:
import warnings
warnings.filterwarnings('ignore')
import pandas as pd
import numpy as np
from matplotlib import style
from matplotlib import pyplot as plt
import seaborn as sns
import statsmodels.formula.api as smf
%matplotlib inline
style.use("fivethirtyeight")
data = pd.read_csv("data/billboard_impact.csv")
data.head()
| deposits | poa | jul | |
|---|---|---|---|
| 0 | 42 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 2 | 52 | 1 | 0 |
| 3 | 119 | 1 | 0 |
| 4 | 21 | 1 | 0 |
deposits là biến kết quả của chúng tôi. POA là biến giả chỉ thành phố Porto Alegre. Khi nó bằng 0 nghĩa là mẫu dữ liệu lấy từ Florianopolis. Jul là một biến giả cho tháng 7 (thời điểm sau can thiệp). Khi biến này bằng 0, nó chỉ mẫu dữ liệu từ tháng 5 (trước can thiệp).
Mô hình ước lượng DID
Để tránh gây nhầm lẫn giữa thời gian và can thiệp, tôi sẽ sử dụng D để chỉ can thiệp và T để chỉ thời gian. Gọi \(Y_D(T)\) là kết quả tiềm năng cho can thiệp D ở thời điểm T. Ở một thế giới siêu tưởng nơi mà chúng ta có thể quan sát giả tưởng, chúng ta sẽ ước lượng tác động can thiệp như sau:
\[\hat{ATET} = E[Y_1(1) - Y_0(1)|D=1]\]Theo đó, tác động nhân quả là hiệu kết quả của nhóm can thiệp tại thời điểm sau can thiệp và cũng nhóm ấy tại thời điểm sau can thiệp nếu chưa từng nhận can thiệp. Tất nhiên chúng ta không thể đo lường theo cách này vì \(Y_0(1)\) là giả tưởng.
Một cách để giải quyết là so sánh trước và sau.
\[\hat{ATET} = E[Y(1)|D=1] - E[Y(0)|D=1]\]Trong ví dụ này, chúng ta muốn so sánh lượng tiền gửi từ POA trước và sau khi đặt biển quảng cáo.
poa_before = data.query("poa==1 & jul==0")["deposits"].mean()
poa_after = data.query("poa==1 & jul==1")["deposits"].mean()
poa_after - poa_before
41.04775
Mô hình ước lượng này cho biết chúng ta nên kì vọng lượng tiền gửi tăng R$ 41,04 sau can thiệp. Nhưng liệu chúng ta có nên tin kết quả này?
Lưu ý rằng \(E[Y(0)|D=1]=E[Y_0(0)|D=1]\), vì thế ước lượng trên đây đặt giả thiết rằng \(E[Y_0(1)|D=1] = E[Y_0(0)|D=1]\). Nó nói rằng khi giả tưởng không có can thiệp, kết quả (của nhóm can thiệp) trong thời điểm sau giống hệt kết quả trong thời điểm trước. Điều này rõ ràng không đúng nếu biến kết quả của bạn tuân theo một xu hướng vận động nào đó. Ví dụ nếu lượng tiền gửi từ POA tăng, \(E[Y_0(1)|D=1] > E[Y_0(0)|D=1]\), nghĩa là kết quả của thời điểm sau lớn hơn thời điểm đầu kể cả khi vắng mặt can thiệp. Tương tự nếu có xu hướng giảm, \(E[Y_0(1)|D=1] < E[Y_0(0)|D=1]\).
Vì thế phương pháp này không chính xác. Một ý tưởng khác là so sánh nhóm can thiệp với một nhóm đối chứng không nhận can thiệp:
\[\hat{ATET} = E[Y(1)|D=1] - E[Y(1)|D=0]\]Trong ví dụ của chúng ta, điều này nghĩa là so sánh tiền gửi từ POA với lượng tiền gửi từ Florianopolis sau thời điểm can thiệp.
fl_after = data.query("poa==0 & jul==1")["deposits"].mean()
poa_after - fl_after
-119.10175000000001
Mô hình ước lượng này cho biết chiến dịch marketing phản tác dụng và làm khách hàng gửi tiền ít hơn một khoản trung bình vào khoảng R$ 119.10.
Lưu ý \(E[Y(1)|D=0]=E[Y_0(1)|D=0]\), vì thế chúng ta giả định rằng có thể thay thế giả tưởng không quan sát được bằng \(E[Y_0(1)|D=0] = E[Y_0(1)|D=1]\). Nhưng lưu ý điều này chỉ đúng nếu hai nhóm có xuất phát điểm tương tự nhau. Ví dụ, nếu ban đầu Florianopolis có lượng tiền gửi nhiều hơn Porto Alegre, điều này không đúng nữa vì \(E[Y_0(1)|D=0] > E[Y_0(1)|D=1]\). Mặt khác, nếu lượng tiền gửi thấp hơn ở Florianopolis, ta có \(E[Y_0(1)|D=0] < E[Y_0(1)|D=1]\).
Vì thế phương pháp này không giúp ích mấy. Để khắc phục nó, ta có thể so sánh theo cả đối tượng và thời gian. Đây là ý tưởng của phương pháp sai khác của biến thiên. Nó hoạt động bằng cách thay thế giả tưởng thiếu vắng bằng:
\[E[Y_0(1)|D=1] = E[Y_1(0)|D=1]\] \[+ (E[Y_0(1)|D=0] - E[Y_0(0)|D=0])\]Cách thức vận hành của nó là lấy kết quả của nhóm can thiệp trước khi can thiệp diễn ra cộng thêm vào một phần xu hướng được ước lượng bằng cách sử dụng nhóm đối chứng \(E[Y_0(1)|T=0] - E[Y_0(0)|T=0]\). Nghĩa là, nó cho rằng nhóm can thiệp, trong giả tưởng vắng mặt can thiệp, sẽ trông giống như nhóm can thiệp trước lúc nhận can thiệp cộng thêm một phần tăng trưởng tương tự như phần tăng trưởng của nhóm đối chứng. Điều quan trọng là cần lưu ý điều này đặt giả thiết rằng xu hướng biến thiên của nhóm can thiệp và nhóm đối chứng là như nhau:
\[E[Y_0(1) − Y_0(0)|D=1] = E[Y_0(1) − Y_0(0)|D=0]\]trong đó vế trái là xu hướng giả tưởng. Bây giờ, chúng ta có thể thay thế ước lượng của giả tưởng trong định nghĩa của tác động can thiệp \(E[Y_1(1)|D=1] - E[Y_0(1)|D=1]\)
\[\hat{ATET} = E[Y(1)|D=1] - (E[Y(0)|D=1]\] \[+ (E[Y(1)|D=0] - E[Y(0)|D=0])\]Sắp xếp lại các phần tử, ta thu được mô hình ước lượng Sai khác của biến thiên cổ điển.
\[\hat{ATET} = (E[Y(1)|D=1] - E[Y(1)|D=0])\] \[- (E[Y(0)|D=1] - E[Y(0)|D=0])\]Tên gọi này xuất phát từ việc nó tính sự sai khác giữa biến thiên của nhóm can thiệp và nhóm đối chứng sau và trước khi có can thiệp.
Bây giờ hãy xem xét đoạn code sau:
fl_before = data.query("poa==0 & jul==0")["deposits"].mean()
diff_in_diff = (poa_after-poa_before)-(fl_after-fl_before)
diff_in_diff
6.524557692307688
Sai khác của biến thiên cho biết chúng ta nên kì vọng mức tiền gửi của mỗi khách hàng tăng R$ 6.52. Lưu ý giả thiết đặt ra bởi sai khác của biến thiên hợp lý hơn 2 mô hình ước lượng trước. Nó chỉ giả định rằng xu hướng tăng trưởng ở 2 thành phố là tương tự nhau. Nhưng nó không yêu cầu chúng phải có cùng mức xuất phát điểm hoặc không biến thiên.
Để mô tả sai khác của biến thiên, chúng ta có thể dùng xu hướng tăng trưởng của nhóm đối chứng để dự báo cho nhóm can thiệp và thiết lập giả tưởng, lượng tiền gửi mà chúng có thể kì vọng nếu không có can thiệp.
plt.figure(figsize=(10,5))
plt.plot(["T5", "T7"], [fl_before, fl_after], label="FL", lw=2)
plt.plot(["T5", "T7"], [poa_before, poa_after], label="POA", lw=2)
plt.plot(["T5", "T7"], [poa_before, poa_before+(fl_after-fl_before)],
label="Giả tưởng", lw=2, color="C2", ls="-.")
plt.legend();
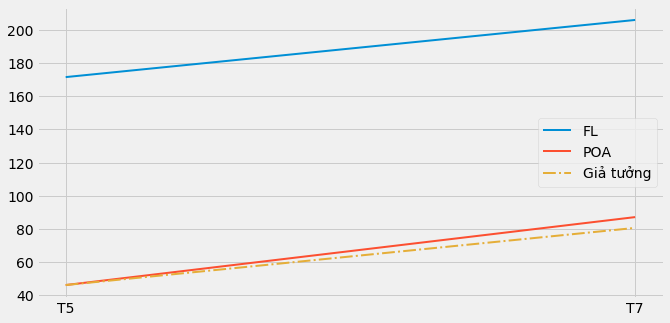
Hãy nhìn khác biệt nhỏ giữa đường màu đỏ và đường nét đứt màu vàng. Nếu tập trung, bạn có thể thấy tác động can thiệp nhỏ đối với Porto Alegre.

Bây giờ bạn có thể hỏi chính mình “liệu mình có thể tin tưởng bao nhiêu vào mô hình ước lượng này? Tôi có quyền yêu cầu được biết các sai số chuẩn !”. Đòi hỏi này chính đáng, vì mô hình ước lượng sẽ trông ngờ nghệch nếu không có chúng. Để làm vậy, chúng ta sẽ dùng một mẹo nhỏ với hồi quy. Cụ thể chúng ta sẽ ước lượng mô hình sau:
\[Y_i = \beta_0 + \beta_1 POA_i + \beta_2 Jul_i + \beta_3 POA_i*Jul_i + e_i\]Lưu ý \(\beta_0\) là xuất phát điểm của nhóm đối chứng. Trong trường hợp của chúng ta, nó là lượng tiền gửi ở Florianopolis trong tháng 5. Nếu chúng ta “bật” biến giả cho thành phố nhận can thiệp, chúng ta thu được \(\beta_1\). Vì thế \(\beta_0 + \beta_1\) là xuất phát điểm của Porto Alegre vào tháng 5, trước khi có can thiệp, và \(\beta_1\) là chênh lệch giữa xuất phát điểm của Porto Alegre so với Florianopolis. Nếu chúng ta “tắt” biến giả POA và “bật” biến giả cho tháng 7, ta thu được \(\beta_0 + \beta_2\), kết quả của Florianópolis trong tháng 7, thời gian sau can thiệp. \(\beta_2\) là xu hướng biến thiên của nhóm đối chứng, vì vậy ta cộng nó vào xuất phát điểm của nhóm đối chứng để thu được kết quả của nhóm đối chứng sau thời điểm can thiệp diễn ra. Hãy nhớ lại, \(\beta_1\) là mức chênh lệch giữa nhóm can thiệp và nhóm đối chứng, \(\beta_2\) là mức biến thiên giữa hai thời điểm trước và sau can thiệp. Cuối cùng nếu “bật” cả 2 biến giả, ta thu được \(\beta_3\). \(\beta_0 + \beta_1 + \beta_2 + \beta_3\) là kết quả của Porto Alegre sau khi nhận can thiệp. Vì thế \(\beta_3\) là mức biến thiên từ tháng 5 đến tháng 7 và khác biệt giữa Florianopolis và POA. Nói cách khác, nó là mô hình ước lượng sai khác của biến thiên.
Nếu bạn không tin tôi, hãy kiểm tra lại. Và hãy lưu ý cách tính sai số chuẩn.
smf.ols('deposits ~ poa*jul', data=data).fit().summary().tables[1]
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 171.6423 | 2.363 | 72.625 | 0.000 | 167.009 | 176.276 |
| poa | -125.6263 | 4.484 | -28.015 | 0.000 | -134.418 | -116.835 |
| jul | 34.5232 | 3.036 | 11.372 | 0.000 | 28.571 | 40.475 |
| poa:jul | 6.5246 | 5.729 | 1.139 | 0.255 | -4.706 | 17.755 |
Xu hướng biến thiên không song song
Một vấn đề khá hiển nhiên với Sai khác của biến thiên là trường hợp giả định xu hướng song song không được đảm bảo. Nếu đường xu hướng biến thiên của nhóm can thiệp khác với xu hướng của nhóm đối chứng, sai khác của biến thiên sẽ bị chệch. Đây là một vấn đề khá phổ biến với dữ liệu không ngẫu nhiên, khi mà quyết định chỉ định can thiệp với một khu vực cụ thể dựa trên tiềm năng đáp ứng của nó đối với can thiệp, hoặc khi can thiệp được chỉ định cho cả khu vực đang hoạt động chưa tốt.
Trong ví dụ marketing của chúng ta, chúng ta quyết định đánh giá tác động biển quảng cáo tại Porto Alegre không phải vì chúng ta cần đánh giá tác động của biển quảng cáo mà đơn giản vì hoạt động marketing tại Porto Alegre đang yếu kém. Có thể vì marketing trực tuyến không hiệu quả tại thành phố này. Trong trường hợp này, mức tăng trưởng chúng ta quan sát thấy tại Porto Alegre khi không có biển quảng cáo có thể thấp hơn mức tăng trưởng mà chúng ta quan sát được ở các thành phố khác. Điều này có thể khiến chúng ta đánh giá thấp tác động của biển quảng cáo ở đó.
Một cách để kiểm chứng điều này là vẽ biểu đồ xu hướng trong quá khứ. Ví dụ giả sử POA có xu hướng giảm nhẹ nhưng Florianopolis đang tăng mạnh. Trong trường hợp này, biểu đồ cho khoảng thời gian trước khi diễn ra can thiệp sẽ bộc lộ các xu hướng này và chúng ta sẽ biết Sai khác của biến thiên không phải mô hình ước lượng đáng tin cậy cho tình huống này.
plt.figure(figsize=(10,5))
x = ["Jan", "Mar", "May", "Jul"]
plt.plot(x, [120, 150, fl_before, fl_after], label="FL", lw=2)
plt.plot(x, [60, 50, poa_before, poa_after], label="POA", lw=2)
plt.plot(["May", "Jul"], [poa_before, poa_before+(fl_after-fl_before)], label="Giả tưởng", lw=2, color="C2", ls="-.")
plt.legend();
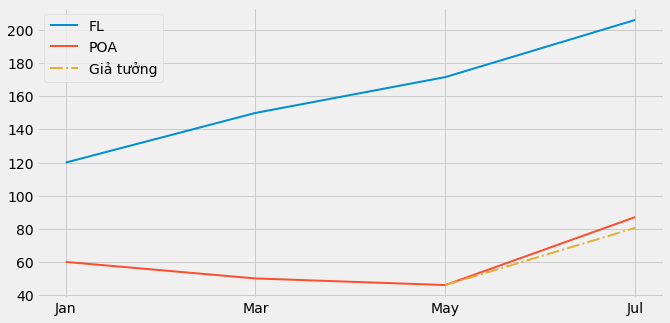
Chúng ta sẽ xem xét cách giải quyết vấn đề này với đối chứng tổng hợp. Nó sẽ sử dụng nhiều thành phố để tạo ra một thành phố tổng hợp có xu hướng vận động gần với thành phố cần nghiên cứu. Nhưng hiện tại, hãy cứ tạm nhớ rằng bạn cần kiểm tra điều kiện xu hướng song song khi áp dụng sai khác của biến thiên.

Vấn đề cuối cùng cần phải nhắc đến là bạn sẽ không thể đặt khoảng tin cậy xung quanh mô hình ước lượng Sai khác của biến thiên nếu bạn chỉ có dữ liệu cộng gộp. Ví dụ thay vì có dữ liệu cho mỗi khách hàng từ Florianópolis hoặc Porto Alegre, bạn chỉ có lượng tiền gửi trước và sau can thiệp cho mỗi thành phố. Trong trường hợp này, bạn sẽ vẫn có thể ước lượng tác động nhân quả bằng Sai khác của biến thiên, nhưng bạn sẽ không biết phương sai của nó. Đó là vì tất cả biến động trong dữ liệu đã biến mất do cộng gộp dữ liệu.
Ý tưởng chủ đạo
Chúng ta đã khám phá một kĩ thuật thông dụng giúp ước lượng tác động nhân quả với đối tượng ở tầm vĩ mô như trường học, thành phố, tiểu bang, quốc gia,… sai khác của biến thiên xem xét đối tượng can thiệp trước và sau can thiệp và so sánh xu hướng biến thiên của kết quả với nhóm đối chứng. Ở đây, chúng ta đã xem xét cách áp dụng phương pháp này trong việc ước lượng tác động của một chiến dịch marketing tại địa bàn thành phố cụ thể.
Cuối cùng, chúng ta đã xem xét thất bại của Sai khác của biến thiên khi xu hướng vận động của nhóm can thiệp và đối chứng không giống nhau. Chúng ta cũng đã thấy vấn đề của sai khác của biến thiên nếu chỉ có dữ liệu cộng gộp.
Tài liệu tham khảo
Tôi muốn dành loạt bài viết này để vinh danh Joshua Angrist, Alberto Abadie and Christopher Walters vì khóa học Kinh tế lượng tuyệt cú mèo của họ. Phần lớn ý tưởng trong loạt bài này được lấy từ các bài giảng của họ được tổ chức bởi Hiệp hội Kinh tế Mĩ. Theo dõi các bài giảng này là những gì tôi làm trong suốt năm 2020 khó nhằn.
Tôi cũng muốn giới thiệu cuốn sách lý thú của Angrist. Chúng cho tôi thấy Kinh tế lượng, hoặc ‘Lượng theo cách họ gọi không chỉ vô cùng hữu ích mà còn rất vui.
Tài liệu tham khảo cuối cùng của tôi là cuốn sách của Miguel Hernan and Jamie Robins. Nó là người bạn đồng hành tin cậy với tôi khi trả lời những câu hỏi nhân quả khó nhằn.
Cuối cùng, tôi cũng muốn tán dương Scott Cunningham và sản phẩm xuất sắc của ông pha trộn Suy Luận Nhân Quả với lời thoại Rap:
Bảng Từ Viết tắt
| Viết tắt | Tiếng Anh | Tiếng Việt |
|---|---|---|
| DID | Difference In Differences | Sai khác của Biến thiên |
Bảng Thuật ngữ
| Thuật ngữ | Tiếng Anh |
|---|---|
| biến giả | dummy, dummy variable |
| chệch | biased |
| code | code |
| dữ liệu cộng gộp | aggregated data |
| dữ liệu không ngẫu nhiên | non-random data |
| dự báo | project |
| giả tưởng | counterfactual |
| học máy | machine learning |
| hồi quy | regression, regress |
| khoảng tin cậy | confidence interval |
| kinh tế lượng | econometrics |
| kết quả tiềm năng | potential outcome |
| mô hình ước lượng | estimator |
| nhóm can thiệp | treated group |
| nhóm đối chứng | control group, untreated group |
| phương sai | variance |
| phần xu hướng | trend component |
| sai khác của biến thiên | difference in difference, diff in diff |
| sai số chuẩn | standard error |
| suy luận nhân quả | causal inference, causal reasoning |
| tác động can thiệp | treatment effect, treatment impact |
| xu hướng giả tưởng | counterfactual trend |
| đối chứng tổng hợp | synthetic control |
Comments