Biến Kiểm Soát

60 GIÂY NHÂN QUẢ - KỲ 1

Bài viết này thuộc chuỗi bài viết về “60 Giây Nhân quả”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây

Để hiểu thêm kiến thức về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “Suy luận Nhân quả với Python” tại đây

---

Chúng ta muốn tìm hiểu biến giải thích X tác động thế nào đến biến kết quả Y. Trong một thế giới lý tưởng, ta chỉ cần nhìn vào mối tương quan giữa X và Y.

Nhưng thực tế không dễ dàng như thế. Có hàng tấn lý do cản trở việc này. Ví dụ nếu có một biến nhiễu W tác động đến cả X và Y như trong biểu đồ dưới đây.

Nếu điều này xảy ra, mối tương quan giữa X và Y mà ta quan sát được từ dữ liệu thô thực ra phản ánh 2 điều:

• Tác động của X lên Y mà chúng ta quan tâm
• Tác động của W lên Y thông qua X mà chúng ta không quan tâm

W tạo ra một lối đi “cửa sau” dẫn X tới Y. Chúng ta có thể đi từ X tới Y bằng cửa chính X → Y hoặc bằng con đường khác mà ta không mong muốn X ← W → Y.

Ví dụ nếu X là học vấn, Y là thu nhập và W là trí tuệ. Chúng ta quan sát thấy những người học vấn cao có thu nhập cao. Một phần là do giáo dục làm tăng thu nhập nhưng còn có lí do khác: nhiều người thông minh chọn học lên cao và những người này vẫn sẽ có thu nhập tốt dù có học nhiều hay không.

Một cách để giải quyết vấn đề này là chặn lối đi cửa sau bằng cách kiểm soát W. Ý tưởng rất đơn giản: chúng ta tiếp tục nhìn vào quan hệ tương quan giữa X và Y sau khi loại bỏ ảnh hưởng của W. Một cách nghĩ khác là chúng ta giữ cố định biến W. Khi đó, chúng ta đóng lại con đường X ← W → Y và chỉ để ngỏ X → Y mà ta quan tâm. Sau khi kiểm soát W, mối liên hệ còn lại giữa X và Y là quan hệ nhân quả (giả sử chỉ có lối đi cửa sau duy nhất thông qua W).

Vậy làm thế nào để có mối liên hệ giữa X và Y sau khi loại bỏ ảnh hưởng của W? “Kiểm soát” ở đây chính là loại bỏ phần biến động của X và Y có thể giải thích bằng W. Bất cứ thành phần nào của X và Y có thể dự đoán bằng W đều cần loại bỏ để đóng lại “cửa sau” và đảm bảo chúng ta đang so sánh những đối tượng có cùng mức độ W.

Nếu W là biến nhị phân (chỉ nhận 2 giá trị, ví dụ 0 hoặc 1), việc kiểm soát W sẽ trông như sau:

Nếu không kiểm soát W, phương trình hồi quy Y theo X cho thấy mối quan hệ đồng biến: mỗi đơn vị tăng thêm của X làm tăng Y thêm 0.67 đơn vị. Nếu mù quáng tin theo, ta sẽ cố làm tăng X nếu muốn tăng kết quả Y.

\[Y =1.2+0.67X+\varepsilon\]

import statsmodels.api as sm # import statsmodels 
# Note the difference in argument order
model = sm.OLS(df.Y, sm.add_constant(df.X)).fit()
model.summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	1.2061	0.283	4.263	0.000	0.645	1.767
X	0.6744	0.132	5.095	0.000	0.412	0.937

Ta có thể kiểm soát biến W bằng cách đưa thẳng nó vào phương trình hồi quy như dưới đây:

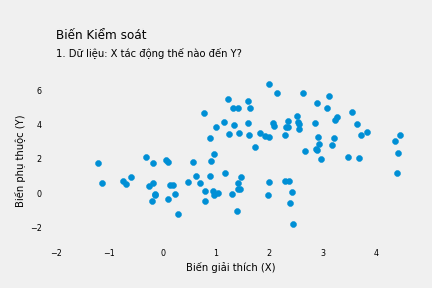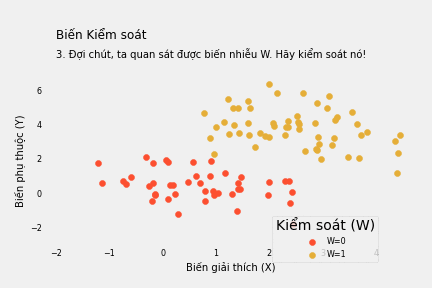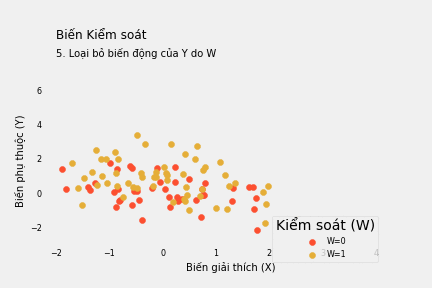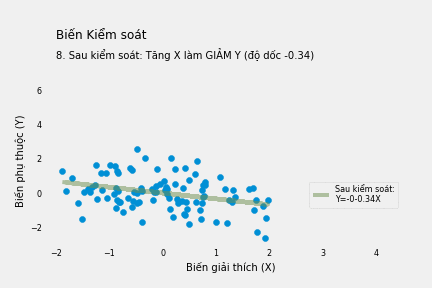
\[Y=0.69-0.34X+3.98W+\varepsilon\]

Kết quả hoàn toàn trái ngược với ban đầu. Mỗi đơn vị tăng thêm của X làm giảm Y 0.34 đơn vị.

model = sm.OLS(df.Y, sm.add_constant(df[['X','W']])).fit()
model.summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	0.6879	0.158	4.348	0.000	0.374	1.002
X	-0.3421	0.098	-3.476	0.001	-0.537	-0.147
W	3.9788	0.261	15.217	0.000	3.460	4.498

Một cách khác để kiểm soát biến nhị phân W là “khử” giá trị trung bình của X và Y theo mỗi giá trị của W trước khi hồi quy Y theo X. Nói cách khác, ta loại bỏ ảnh hưởng của W đối với cả X và Y trước khi xem xét mối quan hệ của 2 biến này.

\[\tilde{Y} = 0-0.34\tilde{X} +\varepsilon\]

trong đó \(\tilde{Y} = Y-E(Y|W) ; \tilde{X} = X-E(X|W)\)

Giống kết quả hồi qua đa biến ở trên, mỗi đơn vị gia tăng của X làm giảm 0.34 đơn vị Y.

model = sm.OLS(df.Y-df.groupby('W').Y.transform('mean'), sm.add_constant(df.X-df.groupby('W').X.transform('mean'))).fit()
model.summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	-1.18e-16	0.095	-1.24e-15	1.000	-0.188	0.188
X	-0.3421	0.098	-3.494	0.001	-0.536	-0.148

Ghi chú:

Ba biến X, Y, và W ở ví dụ trên đã được tạo lập như sau:

\[X= 0.5+ 2W+ \nu; \nu \sim N(0,1)\] \[Y= 1 -0.5X+4W+ \varepsilon; \varepsilon \sim N(0,1)\]

Hệ số “thực” của quan hệ nhân quả giữa X và Y là -0.5.

import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np

# Set size
size=100
np.random.seed(0)

# Biến kiểm soát
W=np.random.randint(0,2,size)

# Biến giải thích
X= 0.5+ 2*W+np.random.normal(0,1,size)
Y= 1 -0.5*X+4*W+np.random.normal(0,1,size)

# Tạo bảng dữ liệu
df=pd.DataFrame({'X':X,'Y':Y,'W':W})
#Demean X
df['Xdm']=df.X-df.groupby('W').X.transform('mean')
#Demean y
df['Ydm']=df.Y-df.groupby('W').Y.transform('mean')