Sai Khác Của Biến Thiên

60 GIÂY NHÂN QUẢ - KỲ 5

Bài viết này thuộc chuỗi bài viết về “60 Giây Nhân quả”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây

Để hiểu thêm kiến thức về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “Suy luận Nhân quả với Python” tại đây

---

Một chính sách mới được đưa ra vào một thời điểm cụ thể đối với một nhóm người, tạm gọi là nhóm (tiếp nhận) Can thiệp. Chúng ta có thể quan sát nhóm người này trước và sau thời điểm chính sách mới (can thiệp) có hiệu lực.

Chúng ta cho rằng chính sách đó đã có tác động nhất định đối với chỉ tiêu kết quả Y. Trong trường hợp lý tưởng, chúng ta chỉ việc so sánh Y trước và sau thời điểm hiệu lực của chính sách và đánh giá được tác động của chính sách đó. Tuy nhiên có nhiều lý do cản trở điều này.

Kết quả Y có thể vẫn tăng với tất cả mọi người trong cùng khoảng thời gian chính sách mới được đưa ra dù người đó có tiếp nhận can thiệp hay không. Điều này được mô tả bởi biều đồ sau đây:

Ví dụ, chúng ta nghiên cứu chính sách chuyển đổi một số phòng làm việc riêng sang khu văn phòng mở và tác động của nó đối với năng suất lao động (Y). Việc chuyển đổi văn phòng diễn ra vào ngày 1/1/2017, vì vậy năm 2016 là thời điểm Trước can thiệp và 2017 là thời điểm Sau can thiệp. Tuy nhiên tình hình kinh tế chung phát triển tốt giữa 2016 và 2017, vì vậy việc năng suất được cải thiện không nhất thiết là do sử dụng văn phòng mở.

Trong tình huông này, sự thay đổi năng suất lao động Y trước và sau can thiệp phản ánh 2 điều: tác động của việc Tiếp nhận Can thiệp lên Y (chúng ta quan tâm) và sự biến thiên theo thời gian của biến Y (mà ta không quan tâm). Thời gian mở ra một lối đi cửa sau từ Can thiệp đến Y. Chúng ta có thể đi từ Tiếp nhận Can thiệp đến Y thông qua Tiếp nhận Can thiệp → Y hoặc Tiếp nhận Can thiệp ← Thời gian → Y.

Một điều tệ hại khác là chúng ta không thể đóng lại lối đi cửa sau bằng cách kiểm soát biến Thời gian nếu chúng ta chỉ xem xét nhóm can thiệp vì khi đó thời gian là biến dự đoán hoàn hảo việc Tiếp nhận Can thiệp (Trước hoặc sau ngày chính sách có hiệu lực). Do đó, nếu ta loại bỏ toàn bộ thành phần Tác động được giải thích bởi Thời gian, chúng ta không còn lại gì cả!

Ta có thể làm gì trong tình huống này? Chúng ta có thể bổ sung nhóm Đối chứng không được chỉ định can thiệp. Trong ví dụ này, ta có thể sử dụng các văn phòng cá nhân được giữ lại từ 2016-2017. Điều này cho phép chúng ta kiểm soát yếu tố Thời gian nhưng lại mở ra một lối đi cửa sau phiền toái khác vì có thể tồn tại khác biệt hệ thống giữa nhóm Can thiệp và Đối chứng. Trong biểu đồ dưới đây, một người chỉ thực sự tiếp nhận can thiệp nếu họ trong nhóm được chỉ định can thiệp VÀ thời gian trôi qua đến thời điểm sau can thiệp. Bên cạnh cửa sau Thời gian, chúng ta có một lối đi cửa sau khác từ Tiếp nhận Can thiệp ← Chỉ định Can thiệp → Y mà chúng ta cần chặn lại:

Chúng ta có thể đồng thời đóng lại các con đường cửa sau đi qua Thời gian và Chỉ định can thiệp bằng cách sử dụng ước lượng Sai khác của Biến thiên (DiD). Ý tưởng là chúng ta nhìn vào Y xem nó thay đổi như thế nào trước và sau khi diễn ra can thiệp đối với nhóm Can thiệp và so sánh với sự thay đổi (biến thiên) của nhóm Đối chứng.

Việc tách biệt sự biến thiên giữa nhóm Đối chứng và Can thiệp là một cách để kiểm soát Chỉ định Can thiệp và đóng lại con đường cửa sau: Tiếp nhận Can thiệp ← Chỉ định Can thiệp → Y. Sau đó ta so sánh sự sai khác giữa biến thiên của nhóm Can thiệp và Đối chứng, đóng lại cửa sau Tiếp nhận Can thiệp ← Thời gian → Y.

Kĩ thuật ước lượng này có thể được mô tả như sau:

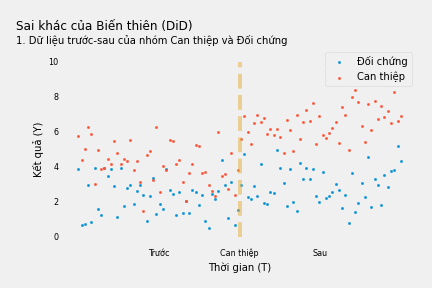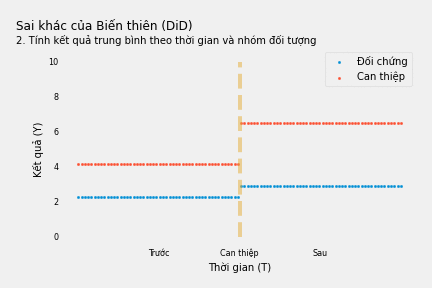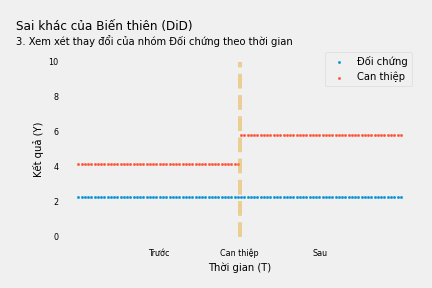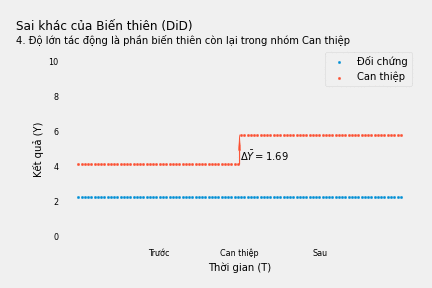
Trong thực hành, chúng ta có thể ước lượng tác động của can thiệp bằng mô hình kinh tế lượng sau đây: \(Y_{it}=2.26+1.69 \times CanThiệp_i \times SauCanThiệp_t+ 1.88\times CanThiệp_i+0.65 \times SauCanThiệp_t\)

\(Y_{it}\) là chỉ số kết quả của cá nhân \(i\) tại thời điểm \(t\). \(CanThiệp_i\) là biến giả nhận giá trị 1 nếu cá nhân \(i\) thuộc nhóm Can thiệp. \(SauCanThiệp_t\) là biến giả nhận giá trị 1 nếu thời điểm \(t\) diễn ra sau khi can thiệp có hiệu lực. Mô hình này cho thấy can thiệp có tác động dương và tính bình quân làm tăng kết quả Y thêm 1.69 đơn vị.

import statsmodels.api as sm # import statsmodels 
df['const']=1
df['CanThiệp']=df['D'].map({'Can thiệp':1,'Đối chứng':0})
df['SauCanThiệp']=df['T'].map({'Sau':1,'Trước':0})
df['CanThiệp*SauCanThiệp']=df.CanThiệp*df.SauCanThiệp
model = sm.OLS(df.Y, df[['const','CanThiệp*SauCanThiệp','CanThiệp','SauCanThiệp']]).fit()
model.summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	2.2565	0.145	15.604	0.000	1.971	2.542
CanThiệp*SauCanThiệp	1.6875	0.289	5.835	0.000	1.117	2.258
CanThiệp	1.8840	0.205	9.212	0.000	1.481	2.287
SauCanThiệp	0.6510	0.205	3.183	0.002	0.248	1.054

Ghi chú

Biến X, Y ở ví dụ trên đã được tạo lập như sau

\[Y_{it}=2+1.5 \times CanThiệp_i \times SauCanThiệp_t + 2\times CanThiệp_i+1 \times SauCanThiệp_t+ \varepsilon_{it}\] \[\varepsilon_{it} \sim N(0,1)\]

Hệ số “thực” của tác động can thiệp là 1.5.

Tạo lập dữ liệu

import pandas as pd
import numpy as np

#Set size
size=200
np.random.seed(0)

#Khởi tạo nhóm
D=np.array(['Can thiệp']*int(size/2)+['Đối chứng']*int(size/2))

#Khởi tạo thời gian so với can thiệp
T=np.array((['Trước']*int(size/4)+['Sau']*int(size/4))*2)

#Tạo lập kết quả
Y= 2+2*(D=="Can thiệp")+1*(T=="Sau") + 1.5*(D=="Can thiệp")*(T=="Sau")+np.random.normal(0,1,size)

#Tạo lập khung dữ liệu
df=pd.DataFrame({'D':D,'T':T,'Y':Y})
#Thời gian
df['t']=df.groupby('D').cumcount()