Biến Đích chung

60 GIÂY NHÂN QUẢ - KỲ 7

Bài viết này thuộc chuỗi bài viết về “60 Giây Nhân quả”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây

Để hiểu thêm kiến thức về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “Suy luận Nhân quả với Python” tại đây

---

Khi Kiểm soát Mô hình Gây hại! - Biến Đích chung

Việc kiểm soát các biến có thể giúp đóng lại cửa sau và xác định tác động nhân quả. Điều này có thể khiến ta cảm thấy nên kiểm soát mọi yếu tố trong trong khả năng của mình. Không hoàn toàn như vậy, kiểm soát biến đôi khi lại gây hại.

Ví dụ, nếu chúng ta có 2 biến X và Y và cho rằng giữa chúng không có mối liên hệ trực tiếp nào. Tuy nhiên, chúng ta nghĩ rằng chúng cùng tác động lên C. Chúng ta gọi C là đích chung vì 2 mũi tên từ X và Y cùng chĩa vào C. Điều này được mô tả bằng biểu đồ nhân quả sau:

Ví dụ, chúng ta có dữ liệu các ứng viên phỏng vấn cho một công việc lập trình. X là kĩ năng lập trình, Y là kĩ năng giao tiếp, và C là kết quả tuyển dụng. Mọi người được nhận vào làm khi kết quả tổng hợp đánh giá khả năng lập trình và giao tiếp vượt quá một ngưỡng nào đó. Vì vậy, các ứng viên trúng tuyển là những người rất giỏi lập trình, hoặc rất giỏi giao tiếp hoặc phải khá cả hai.

Chúng ta không cho rằng X và Y liên quan đến nhau nhưng vẫn hoài nghi và quyết định nhìn vào dữ liệu. Và vì biết rằng chúng cùng liên quan đến C, ta quyết định kiểm soát C.

Nhưng thực ra chúng ta không nên kiểm soát C chút nào vì chẳng có cửa sau nào để đóng lại. Vì các mũi tên cùng hướng vào C, đường đi X → C ← Y trên thực tế đã tự đóng lại. Kiểm soát C sẽ mở lại cánh cửa đó và cản trở chúng ta tìm hiểu tác động thực sự của X lên Y.

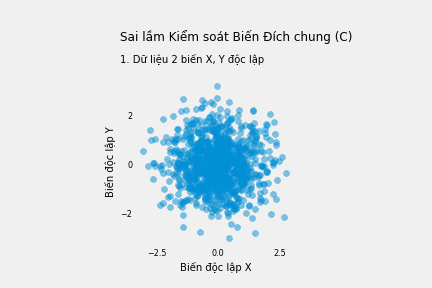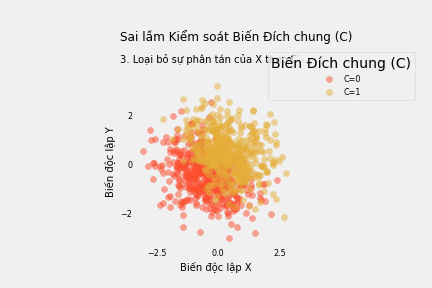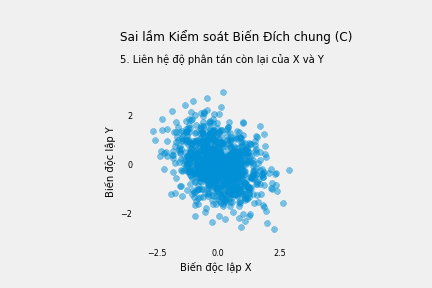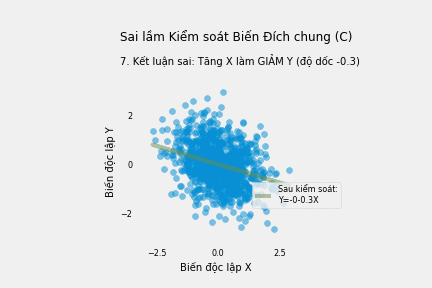
Khi kiểm soát kết quả chung, chúng ta sẽ tạo ra mối tương quan giả giữa X và Y. X và Y không hề liên quan đến nhau nhưng vì C đặt ra ràng buộc cho tổng của X và Y, X và Y trở nên liên quan khi xem xét nhóm người có cùng mức độ kết quả C. Ngay cả khi X và Y liên quan đến nhau, việc kiểm soát C sẽ làm sai lệch kết quả, vì chúng ta đã mở lại lối đi cửa sau.

Hình động dưới đây giải thích điều này:

Ghi chú

Hai biến độc lập X, Y và kết của chung C trên đây đã được tạo lập như sau:

\[X=\nu; \nu \sim N(0,1)\] \[Y=\mu; \nu \sim N(0,1)\] \[C=X+Y+\varepsilon; \varepsilon \sim N(0,1)\]

X và Y không có mối tương quan với nhau. Hệ số góc của phương trình hồi quy Y theo X không có ý nghĩa thống kê (trị số p=0.32):

import statsmodels.api as sm # import statsmodels 
model = sm.OLS(df.Y, sm.add_constant(df.X)).fit()
model.summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	0.0122	0.031	0.398	0.690	-0.048	0.072
X	-0.0309	0.031	-0.996	0.320	-0.092	0.030

Tuy nhiên hệ số góc của X trở nên có ý nghĩa thống kê (trị số p =0.000) khi ta kiểm soát kết quả chung C và ta thu được mối tương quan giả - tăng X làm giảm Y:

model = sm.OLS(df.Y, sm.add_constant(df[['X','C']].astype(float))).fit()
model.summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	-0.5683	0.039	-14.737	0.000	-0.644	-0.493
X	-0.2987	0.029	-10.200	0.000	-0.356	-0.241
C	1.1720	0.058	20.267	0.000	1.058	1.285

Tạo lập dữ liệu

import pandas as pd
import numpy as np

#Set size
size=1000
np.random.seed(0)

#Biến kiểm soát

X= np.random.normal(0,1,size)
Y= np.random.normal(0,1,size)
C=(X+Y+np.random.normal(0,1,size))>0

#Tạo bảng dữ liệu
df=pd.DataFrame({'X':X,'Y':Y,'C':C})
#Demean X
df['Xdm']=df.X-df.groupby('C').X.transform('mean')
#Demean y
df['Ydm']=df.Y-df.groupby('C').Y.transform('mean')