Kiểm Soát Sau Can Thiệp

60 GIÂY NHÂN QUẢ - KỲ 8

Bài viết này thuộc chuỗi bài viết về “60 Giây Nhân quả”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây

Để hiểu thêm kiến thức về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “Suy luận Nhân quả với Python” tại đây

---

Khi Kiểm soát Mô hình Gây hại! - Biến Hậu Can thiệp

Việc kiểm soát biến có thể giúp đóng lại cửa sau và xác định tác động nhân quả. Điều này có thể khiến ta cảm thấy nên kiểm soát mọi yếu tố trong trong khả năng của mình. Không hẳn như vậy, kiểm soát biến đôi khi lại gây hại.

Ví dụ, nếu ta cho rằng biến (can thiệp) X có tác động lên biến Y. Tuy nhiên tác động đó thông qua C và C có tác động lên Y. Ta gọi C là biến Hậu Can thiệp vì nó cũng chịu tác động của tác nhân (can thiệp) X.

Ví dụ X là giá thuốc lá, Y là tình hình sức khỏe và C là số điếu thuốc lá được hút. Giá thuốc lá có tác động lên sức khỏe vì nó làm giảm lượng thuốc được hút.

Bây giờ, ta muốn đo lường tác động của X lên Y. Vì biết C cũng chi phối Y, ta quyết định kiểm soát cả C.

Thực ra ta không nên kiểm soát C vì C chẳng đóng lại kênh tác động cửa sau nào. C nằm trên kênh tác động mà chúng ta muốn nghiên cứu X → C → Y. Nếu kiểm soát C, ta chẳng những không đóng lại cửa sau mà còn đóng luôn cửa trước (kênh tác động muốn nghiên cứu). Kết quả là X trông như thể không có tác động lên Y dù thực tế là có.

Hãy xem hình động dưới đây:

Cần lưu ý rằng kiểm soát biến hậu can thiệp gây ra rắc rối, ngay cả khi nó không tác động lên Y! Xem xét biến hậu can thiệp C không tác động lên Y nhưng tương quan với C thông qua biến nhiễu (W) C ← W → Y, như biểu đồ dưới đây:

Vì ở đây C là một biến đích chung, kênh tác động cửa sau X → C ← W đã bị chặn. Tuy nhiên khi kiểm soát C, kênh tác động này bị mở lại và X → C ← W → Y trở thành X-W -> Y. Kênh tác động cửa sau mới mở này sẽ gây ra rắc rối cho việc đánh giá tác động nhân quả.

Ghi chú

Các biến X, Y, C ở trên đã được tạo lập như sau

\[X=1+\nu; \nu \sim N(0,1)\] \[C=X>0\] \[Y=1+2.5\times C+\varepsilon; \varepsilon \sim N(0,1)\]

Khi không kiểm soát, X và Y có mối quan hệ tương quan mạnh. Mỗi đơn vị tăng thêm của X làm tăng 0.66 đơn vị Y

\[Y=2.23+0.66X+\epsilon\]

sm.OLS(df.Y, sm.add_constant(df.X)).fit().summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	2.2361	0.113	19.844	0.000	2.014	2.458
X	0.6638	0.076	8.717	0.000	0.514	0.814

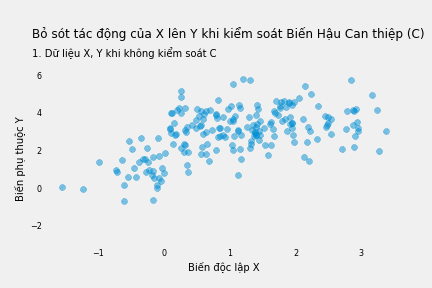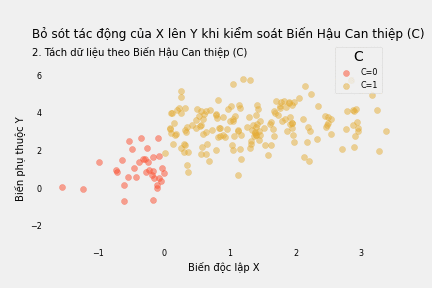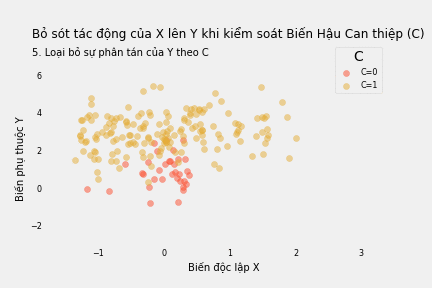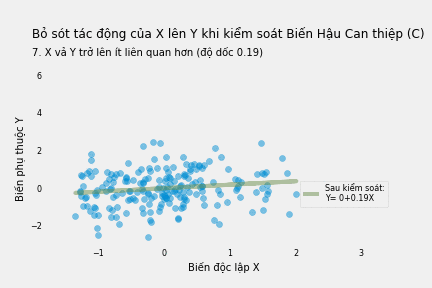
Khi kiểm soát C, quan hệ tương quan giữa X và Y giảm. Mỗi đơn vị tăng thêm của X chỉ làm tăng 0.19 đơn vị Y. Điều này là do biến Hậu Can thiệp C đã hấp thụ mất một phần tác động của X lên Y.

\[Y=1.07+0.19X+2.01C+ϵ\]

sm.OLS(df.Y, sm.add_constant(df[['X','C']].astype(float))).fit().summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	1.0783	0.164	6.573	0.000	0.755	1.402
X	0.1859	0.085	2.187	0.030	0.018	0.353
C	2.0116	0.231	8.704	0.000	1.556	2.467

Tạo lập dữ liệu

import pandas as pd
import numpy as np
import statsmodels.api as sm # import statsmodels 

# # Set size
size=200
np.random.seed(0)

# Biến kiểm soát

X= 1+np.random.normal(0,1,size)
C=X>0
Y=1+2.5*C+np.random.normal(0,1,size)

# Tạo bảng dữ liệu
df=pd.DataFrame({'X':X,'Y':Y,'C':C})
#Demean X
df['Xdm']=df.X-df.groupby('C').X.transform('mean')
#Demean y
df['Ydm']=df.Y-df.groupby('C').Y.transform('mean')