Hiệu Ứng Cố Định

60 GIÂY NHÂN QUẢ - KỲ 4

Bài viết này thuộc chuỗi bài viết về “60 Giây Nhân quả”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây

Để hiểu thêm kiến thức về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “Suy luận Nhân quả với Python” tại đây

---

Chúng ta cho rằng X chi phối Y và muốn đánh giá độ lớn của tác động. Trong điều kiện lý tưởng, chúng ta chỉ việc nhìn vào dữ liệu và xem xét mối quan hệ giữa X và Y. Tuy nhiên có nhiều lý do để cản trở việc này. Ví dụ khác biệt giữa các cá nhân dẫn đến khác biệt về độ lớn của X và Y. Ta có thể theo dõi biểu đồ nhân quả dưới đây:

Trong biểu đồ trên, đặc tính cá nhân bao gồm tất cả đặc điểm cố định theo thời gian của các đối tượng (con người, doanh nghiệp, thành phố, quốc gia) mà ta đang nghiên cứu. Nếu điều này xảy ra, mối quan hệ mà chúng ta quan sát được giữa X và Y trong dữ liệu (mối quan hệ thô) phản ánh 2 điều: tác động của X lên Y (chúng ta quan tâm) và tác động chung của đặc tính cá nhân lên X và Y (chúng ta không quan tâm). Đặc tính cá nhân mở ra đường đi “cửa sau” từ X đến Y. Chúng ta có thể đi từ X đến Y thông qua con đường X → Y hoăc X ← Đặc tính cá nhân → Y. Chúng ta chỉ muốn nghiên cứu con đường đầu tiên mà thôi.

Ví dụ, nếu X là trình độ học vấn của CEO và Y là lợi nhuận năm của doanh nghiệp. Một số loại hình doanh nghiệp làm ăn hiệu quả hơn và đồng thời ta quan sát được các doanh nghiệp này nhiều hoặc ít khả năng sử dụng CEO có trình độ học vấn cao hơn. Chúng ta không biết đặc tính cụ thể nào của doanh nghiệp tác động đến cả 2 nhân tố này và thực ra chúng ta cũng không cần đo lường tất cả các nhân tố đó. Ước lượng hiệu ứng cố định trả lời câu hỏi, với mỗi doanh nghiệp cố định, khi so sánh lợi nhuận hàng năm khi sử dụng CEO học vấn cao và không có học vấn cao thì năm nào thu được lợi nhuận cao hơn. Muốn vậy, chúng ta phải quan sát được số liệu lợi nhuận của mỗi doanh nghiệp nhiều lần (dữ liệu bảng) để có nhiều thời kì so sánh.

Chúng ta có thể đóng lại lối đi cửa sau (qua đặc tính cá nhân) bằng cách sử dụng hiệu ứng cố định nếu ta quan sát được các cá nhân qua các thời kì khác nhau. Ý tưởng là chúng ta nhìn vào quan hệ giữa X và Y với mỗi đối tượng cố định. Một cách nghĩ khác là ta kiểm soát luôn đối tượng được nghiên cứu. Khi đó, ta đóng lại con đường X ← Đặc tính cá nhân → Y và chỉ giữ lại con đường X → Y mà chúng ta quan tâm! Sau khi kiểm soát đặc tính cá nhân, quan hệ còn lại giữa X và Y là quan hệ nhân quả (giả thiết đặc tính cá nhân là lối đi cửa sau duy nhất).

Làm thế nào để nghiên cứu quan hệ giữa X và Y trên cùng đối tượng? Cách làm là loại bỏ các biến động trong dữ liệu về X và Y được giải thích bởi biến định danh cá nhân nhằm đóng lại lối đi cửa sau và đảm bảo chúng ta đang so sánh X và Y trên cùng đối tượng.

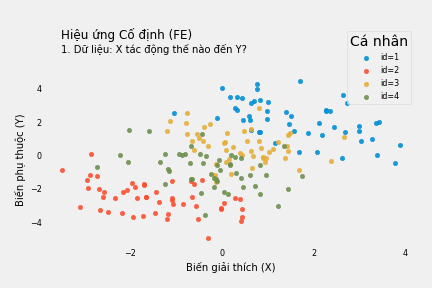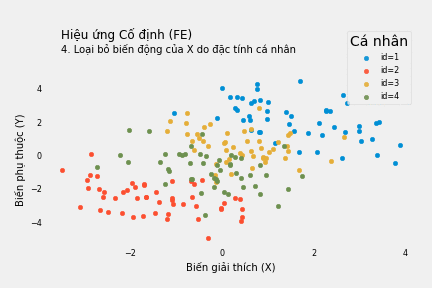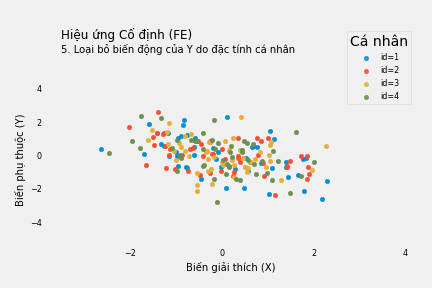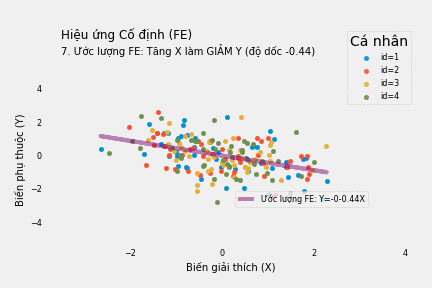
Bỏ qua đặc tính của cá nhân, phương trình hồi quy Y theo X cho thấy mối quan hệ đồng biến: mỗi đơn vị tăng thêm của X làm tăng Y thêm 0.65 đơn vị. Nếu mù quáng tin theo, ta sẽ cố làm tăng X nếu muốn tăng kết quả Y.

\[Y_{it} =-0.21+0.65X_{it}+\varepsilon_{it}\]

import statsmodels.api as sm # import statsmodels 
# Note the difference in argument order
model = sm.OLS(df.Y, sm.add_constant(df.X)).fit()
model.summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	-0.2093	0.126	-1.661	0.098	-0.458	0.039
X	0.6465	0.084	7.693	0.000	0.481	0.812

Dù không quan sát được hết các đặc tính cố định theo cá nhân, ta vẫn có thể kiểm soát chúng bằng cách loại bỏ giá trị trung bình khỏi X và Y trước khi hồi quy.

Kết quả hồi quy tuyến tính giữa Y* và X* cho ta biết việc tăng X thực ra làm giảm giá trị của Y

\[Y^*_{it}=0.00-0.44X^*_{it}+\nu_{it}\]

trong đó

\[Y^*_{it}=E(Y_{it}|i), X^*=E(X_{it}|i)\]

model = sm.OLS(df.Y-df.groupby('id').Y.transform('mean'), sm.add_constant(df.X-df.groupby('id').X.transform('mean'))).fit()
model.summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	-1.409e-16	0.066	-2.13e-15	1.000	-0.131	0.131
X	-0.4419	0.065	-6.770	0.000	-0.571	-0.313

Ghi chú 1:

Biến X, Y ở ví dụ trên đã được tạo lập như sau

\[X_{it}= 0.5+ P_{i}+ \nu_{it}; \nu_{it} \sim N(0,1)\] \[Y_{it}= 1 -0.5X_{it}+2P_i+ \varepsilon_{it}; \varepsilon_{it} \sim N(0,1)\]

Trong đó \(i,t\) lần lượt là các chỉ số cho cá nhân và thời gian. \(P_i\) là hệ số cố định chỉ phụ thuộc vào cá nhân. Cụ thể trong trường hợp này, \(P\) nhận giá trị 1, -2, 0, -1 nếu chỉ số cá nhân \(i\) lần lượt là 1, 2, 3, hoặc 4.

Hệ số “thực” của quan hệ nhân quả giữa X và Y là -0.5.

Ghi chú 2:

Sai số của ước lượng trong phương pháp trình bày trên đây chưa chính xác và cần điều chỉnh hệ số tự do. Nếu quan tâm đến việc ước lượng cả hệ số và sai số của tác động nhân quả, ta có thể sử dụng thư viện linearmodels:

from linearmodels.panel import PanelOLS
panel=df.set_index(['id','t'])
mod = PanelOLS(panel.Y,panel.X,entity_effects=True)
result = mod.fit(cov_type='homoskedastic', cluster_entity=True,debiased=True)
result.summary.tables[1]

Parameter Estimates

	Parameter	Std. Err.	T-stat	P-value	Lower CI	Upper CI
X	-0.4419	0.0658	-6.7180	0.0000	-0.5716	-0.3122

Tạo lập dữ liệu

pip install linearmodels
import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np

#Set size
size=200
np.random.seed(0)

#Tạo lập hệ cố định cho mỗi cá nhân
P=np.array([1,-2,0,-1]*int(size/4))

#Tạo lập biến phụ thuộc và giải thích
X=0.5+P+np.random.normal(0,1,size)
Y= 1-0.5*X+2*P+np.random.normal(0,1,size)

#Tạo lập khung dữ liệu
df=pd.DataFrame({'X':X,'Y':Y,'P':P})

#Tạo chỉ số cá nhân và thời gian
df['id']=df.index%4+1
df['t']=df.index.map(lambda x:int(x/4)+1)

#Khử giá trị trung bình theo id
df['Xdm']=df.X-df.groupby('id')['X'].transform('mean')
df['Ydm']=df.Y-df.groupby('id')['Y'].transform('mean')