Thiết Kế Hồi Quy Gián Đoạn

60 GIÂY NHÂN QUẢ - KỲ 6

Bài viết này thuộc chuỗi bài viết về “60 Giây Nhân quả”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây

Để hiểu thêm kiến thức về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “Suy luận Nhân quả với Python” tại đây

---

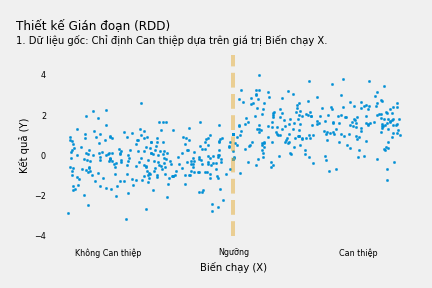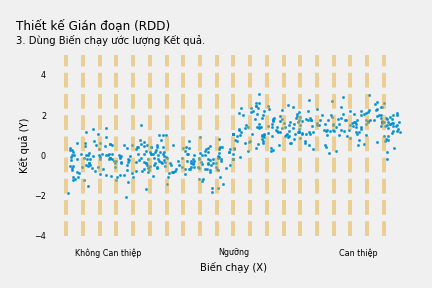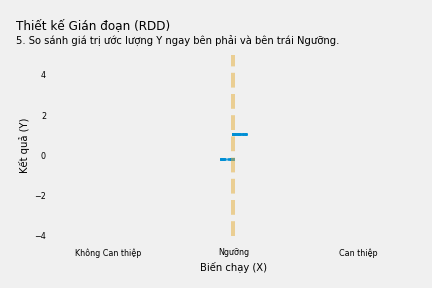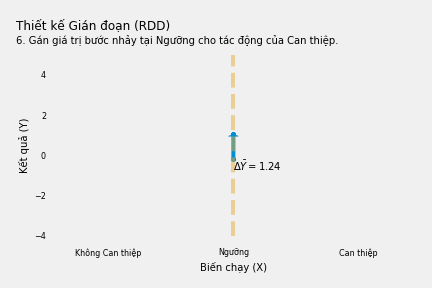
Chúng ta xem xét một Can thiệp chính sách có khả năng tác động lên Biến Kết quả Y và muốn đánh giá độ lớn của tác động đó. Trong điều kiện lý tưởng, chúng ta chỉ cần nhìn vào mối tương quan giữa Can thiệp và Y từ dữ liệu. Nhưng có nhiều lý do cản trở việc này. Ví dụ một số nhóm người có biến kết quả Y cao hoặc thấp hơn người khác dù có tiếp nhận Can thiệp của chính sách hay không. Thực tế trong trường hợp này, Can thiệp được chỉ định dựa vào một Biến Chạy (X). Nếu giá trị của Biến chạy vượt ngưỡng nhất định, người đó được chỉ định nhận Can thiệp và không nếu ngược lại. Tuy nhiên bản thân Biến chạy có khả năng giải thích Y như biểu diễn trong biểu đồ dưới đây:

Ví dụ, Can thiệp là việc thi đỗ vào trường (THPT) chuyên, Y là việc thi đỗ đại học và Biến chạy là điểm thi vào trường chuyên. Thí sinh có điểm thi vượt 90 điểm (trên thang 100) được nhận vào trường chuyên và thí sinh dưới 90 không được nhận. Việc học trường chuyên có khả năng hỗ trợ học sinh thi đại học tốt hơn. Tuy nhiên học sinh có điểm thi vào trường chuyên cao vẫn sẽ có khả năng đỗ đại học cao hơn (dù các em có học trường chuyên hay không).

Khi điều này xảy ra, mối quan hệ giữa biến Can thiệp và Y phản ánh 2 điều: tác động của Can thiệp lên Y (chúng ta quan tâm) và tác động chung của Biến chạy lên Can thiệp và Y (chúng ta không quan tâm). Biến chạy mở ra lối đi cửa sau từ Can thiệp đến Y. Chúng ta có thể đi từ Can thiệp đến Y qua con đường trực tiếp Can thiệp → Y hoặc Can thiệp ← Vượt ngưỡng ← Biến chạy → Y.

Chúng ta có thể đóng lại cửa sau bằng cách kiểm soát Biến chạy. Cách tốt nhất để làm việc này là xem xét Biến chạy giải thích Y như thế nào rồi tập trung vào các điểm dữ liệu ngay xung quanh “ngưỡng”. Điều này đảm bảo chúng ta thực sự so sánh những người nhận can thiệp và không nhận can thiệp có giá trị Biến Chạy xấp xỉ nhau, hay nói cách khác, chúng ta thực sự kiểm soát “Biến chạy”.

Tại sao cần so sánh các điểm dữ liệu ngay xung quanh ngưỡng mà không trực tiếp kiểm soát Biến chạy theo cách thông thường? Bởi vì trong số những người nằm ở ngay gần ngưỡng, việc họ nằm ngay trên hoặc ngay dưới ngưỡng gần giống việc được chỉ định ngẫu nhiên. Và chính sự gần giống ngẫu nhiên này đóng lại các lối đi cửa sau nếu có cả khi chúng ta không nhận ra chúng. Ví dụ nếu biểu đồ nhân quả thực ra trông như sau:

Trong tình huống này, bằng việc tập trung vào khu vực ngay xung quanh ngưỡng, chúng ta có thể cô lập con đường Vượt ngưỡng → Can thiệp → Y và có thể bỏ qua con đường cửa sau Can thiệp ← W → Y.

Biểu đồ dưới đây giải thích cách thực hiện phương pháp này.

Lưu ý nếu Biến chạy là thời gian thì nó được gọi là Chuỗi Thời gian gián đoạn hoặc Nghiên cứu Sự kiện. Tất nhiên,trong các nghiên cứu này việc giới hạn lân cận ngưỡng không thực sự đóng lại hoàn toàn con đường Tác động ← Vượt ngưỡng ← Biến chạy → Y, vì thời gian trước và sau “ngưỡng” là khác nhau và nhiều sự vật, sự việc khác đã thay đổi!

Ghi chú 1

Biến X, Y ở ví dụ trên đã được tạo lập như sau

\[Y=0.2\times X+1.5\times D-0.1\times X\times D+ \varepsilon_{it}; \varepsilon_{it} \sim N(0,1)\]

Trong đó D là biến nhị phân nhận giá trị 1 nếu X vượt ngưỡng 0 (\(X\geq0\)) và nhận giá trị 0 nếu ngược lại.

Ghi chú 2

Có nhiều kĩ thuật khác nhau để ước lượng giá trị Y theo X và nội dung trên đây chỉ giới thiệu một kĩ thuật đơn giản hóa. Bạn đọc có thể tham khảo các nội dung chuyên sâu hơn tại SUY LUẬN NHÂN QUẢ VỚI PYTHON - KỲ 16.

Tạo lập dữ liệu

import pandas as pd
import numpy as np

#Set size
size=500
np.random.seed(0)

# Tạo biến chạy
X=np.random.uniform(-1,1,size=size)

#Tạo lập biến kết quả
Y = .2*X+1.5*(X>=0)-.1*X*(X>=0)+np.random.normal(0,1,size)

#Tạo lập khung dữ liệu
df=pd.DataFrame({'X':X,'Y':Y})

#Phân nhóm dữ liệu
df['g']=df.X.map(lambda x: int((x+1)/0.1))