Biến Công Cụ

60 GIÂY NHÂN QUẢ - KỲ 3

Bài viết này thuộc chuỗi bài viết về “60 Giây Nhân quả”. Hãy cùng đọc thêm các bài viết có cùng chủ đề tại đây

Để hiểu thêm kiến thức về Suy luận Nhân quả, hãy cùng tìm đọc chuỗi bài viết về “Suy luận Nhân quả với Python” tại đây

---

Chúng ta cho rằng X chi phối Y và muốn đánh giá độ lớn của tác động. Trong điều kiện lý tưởng, chúng ta chỉ việc dùng dữ liệu và xem xét mối quan hệ giữa X và Y. Tuy nhiên có nhiều lý do để cản trở việc này. Ví dụ, nếu có biến nhiễu W tác động cả X và Y như mô tả biểu đồ nhân quả dưới đây:

Trong trường hợp này, mối quan hệ giữa X và Y mà ta quan sát được từ dữ liệu thô thực ra phản ánh 2 điều:

• Tác động của X lên Y mà chúng ta quan tâm
• Tác động của W lên Y thông qua X mà chúng ta không quan tâm

W tạo ra một lối đi “cửa sau” dẫn X tới Y. Chúng ta có thể đi từ X tới Y bằng cửa chính X → Y hoặc bằng con đường khác mà ta không mong muốn X ← W → Y.

Tuy nhiên trong biểu đồ này, chúng ta quan sát được biến Z tác động lên X nhưng không có lối đi cửa sau nào dẫn từ Z đến Y một khi ta chặn lại con đường qua X. Trong trường hợp này, nếu ta cô lập phần biến động của X được giải thích bởi Z, không còn lối đi cửa sau qua W vì Z không liên quan đến W.

Ví dụ, X là thu nhập của bố mẹ và Y là điều kiện sức khỏe của trẻ. W là điều kiện sức khỏe của bố mẹ, nhân tố có thể chi phối cả điều kiện sức khỏe của trẻ (một số bệnh tật do di truyền hoặc truyền nhiễm) và thu nhập của bố mẹ (người ốm yếu khó có thể làm việc tốt).

Z có thể là một chỉ định ngẫu nhiên cho một chương trình phúc lợi phát tiền dưới dạng séc cho bố mẹ hàng tháng. Việc phát séc làm tăng thu nhập nhưng không liên quan gì đến điều kiện sức khỏe của bố mẹ (vì chương trình được chỉ định ngẫu nhiên) và chúng ta không còn cần lo lắng về lối đi cửa sau thông qua điều kiện sức khỏe của bố mẹ.

Một cách để giải quyết vấn đề là sử dụng Z làm biến công cụ cho X. Ý tưởng là chúng ta cô lập phần biến động trong dữ liệu gây ra bởi Z. Vì Z không liên quan đến W, W không còn gây ra phiền toái nữa. Cụ thể hơn X ← W → Y là lối đi cửa sau nhưng X* ← W → Y* thì không, với X* và Y* là các thành tố của X và Y được lý giải bới Z. Vì thế, chúng ta có thể ước lượng tác động X* → Y* với biến công cụ.

Điều này hơi trái ngược với việc kiểm soát biến. Thay vì loại bỏ toàn bộ thành tố của X và Y được giải thích bằng biến kiểm soat, chúng ta loại bỏ toàn bộ các thành tố của X và Y không được giải thích bởi biến công cụ.

Nếu Z là biến nhị phân (chỉ nhận 2 giá trị 0 và 1), việc sử dụng Z làm biến công cụ cho X diễn ra như sau:

Nếu không giải quyết vấn đề phát sinh do biến nhiễu W (không quan sát được), phương trình hồi quy Y theo X cho thấy mối quan hệ đồng biến: mỗi đơn vị tăng thêm của X làm tăng Y thêm 0.40 đơn vị. Nếu mù quáng tin theo, ta sẽ cố làm tăng X nếu muốn tăng kết quả Y.

\[Y =-1.14+0.40X+\varepsilon\]

import statsmodels.api as sm # import statsmodels 
# Note the difference in argument order
model = sm.OLS(df.Y, sm.add_constant(df.X)).fit()
model.summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	-1.1369	0.185	-6.159	0.000	-1.501	-0.773
X	0.4037	0.064	6.285	0.000	0.277	0.530

Nếu quan sát được biến Z thỏa mãn các điều kiện trong biểu đồ nhân quả ở trên, chúng ta có thể khắc phục sai lầm.

Chúng ta dùng hồi quy tuyến tính để dự báo giá trị X* và Y* của biến X và Y. Bằng cách này, chúng ta loại bỏ các thành tố tạo nên X và Y không được giải thích bởi X và Y. Các thành tố này có thể gây rắc rối do liên quan đến biến nhiễu W mà ta không quan sát được).

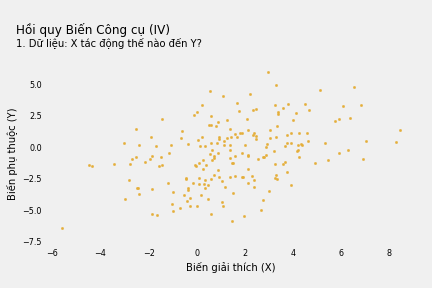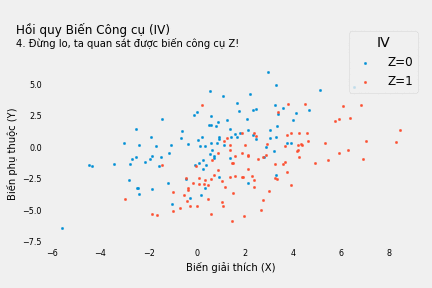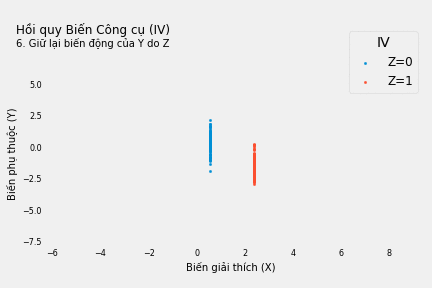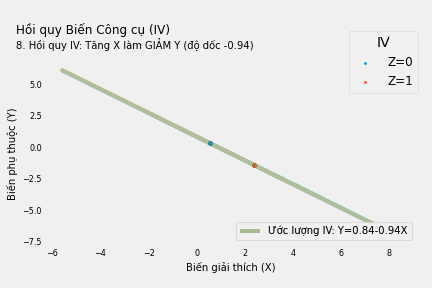
Hồi quy tuyến tính giữa Y* và X* cho ta biết việc tăng X thực ra làm giảm giá trị của Y

\[Y^*=0.84-0.94X^*+\nu\]

trong đó

\[Y^*=E(Y|Z), X^*=E(X|Z)\]

df['X*']=sm.OLS(df.X, sm.add_constant(df.Z)).fit().predict()
df['Y*']=sm.OLS(df.Y, sm.add_constant(df.Z)).fit().predict()
model = sm.OLS(df['Y*'], sm.add_constant(df['X*'])).fit()
model.summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	0.8403	4.29e-17	1.96e+16	0.000	0.840	0.840
X*	-0.9433	2.48e-17	-3.8e+16	0.000	-0.943	-0.943

Ghi chú 1

Biến X, Y ở ví dụ trên đã được tạo lập như sau (biến Z là biến nhị phân ngẫu nhiên):

\[X= 0.5+ 2W+ 2Z+ \nu; \nu \sim N(0,1)\] \[Y= 1 -X+4W+ \varepsilon; \varepsilon \sim N(0,1)\]

Hệ số “thực” của quan hệ nhân quả giữa X và Y là -1.

Tạo lập dữ liệu mô phỏng

pip install linearmodels
import warnings
warnings.filterwarnings('ignore')

import pandas as pd
import numpy as np

#Set size
size=200
np.random.seed(0)
#Biến công cụ ngẫu nhiên ngoại sinh
Z=np.random.randint(0,2,size)
#Biến không quan sát ngẫu nhiên
W=np.random.normal(0,1,size)
#Biến giải thích X và biến phụ thuộc Y đều tương quan với biến thiếu W
m,n,p=0.5,2,2
X = m+n*W +p*Z+ np.random.normal(0,1,size)
a,b,c=(1,-1,4)
Y = a+b*X + c*W+np.random.normal(0,1,size)

#Create Data Frame
df=pd.DataFrame({'X':X,'Y':Y,'Z':Z})
#Calculate X, Y mean, grouped by Z value
df['Xavg']=df.groupby('Z')['X'].transform('mean')
df['Yavg']=df.groupby('Z')['Y'].transform('mean')
#Split data by Z values
df0=df[df.Z==0]
df1=df[df.Z==1]

Ghi chú 2

Nội dung trên đây đơn giản hóa thao tác tính toán với biến công cụ và tập trung ước lượng độ lớn của tác động nhân quả và bỏ qua sai số của ước lượng.

Trong thực tế, biến công cụ thường được sử dụng trong Hồi quy Bình phương Tối thiểu Hai bước (2SLS) (xem thêm SUY LUẬN NHÂN QUẢ VỚI PYTHON - KỲ 8: Biến Công cụ). Với Python, 2SLS có thể thực hiện với thư viện statsmodels hoặc linearmodels.

from statsmodels.sandbox.regression.gmm import IV2SLS  
ivreg = IV2SLS(df.Y,sm.add_constant(df.X),sm.add_constant(df.Z)).fit()
ivreg.summary().tables[1]

	coef	std err	t	P>|t|	[0.025	0.975]
const	0.8403	0.540	1.556	0.121	-0.225	1.905
X	-0.9433	0.313	-3.017	0.003	-1.560	-0.327

from linearmodels.iv import IV2SLS
df['const']=1
ivreg=IV2SLS(df.Y,df.const,df.X,df.Z).fit(cov_type='unadjusted',debiased=True)
ivreg.summary.tables[1]

Parameter Estimates

	Parameter	Std. Err.	T-stat	P-value	Lower CI	Upper CI
const	0.8403	0.5401	1.5559	0.1213	-0.2248	1.9055
X	-0.9433	0.3126	-3.0173	0.0029	-1.5598	-0.3268